Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vázané extrémy funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 01. 2019 10:49 — Editoval AterCZ (05. 01. 2019 10:50)
Vázané extrémy funkce dvou proměnných
Zdravím,
snažím se vyřešit příklad. Mohu poprosit o pomoc?
Najdi vázané lokální extrémy fce dvou proměnných 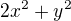 při vazební podmínce
při vazební podmínce 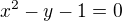
Úprava vazební podmínky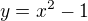
Dosazení do rovnice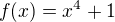
První derivace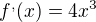
Bod podezřelý z extrému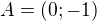
Druhá derivace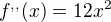
Dosazení A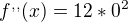
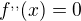
V bodě A má být lokální minimum, samotný bod A je dle výsledků správně.
Offline
- (téma jako vyřešené označil(a) AterCZ)
#2 05. 01. 2019 11:09
Re: Vázané extrémy funkce dvou proměnných
↑ AterCZ:
Ahoj.
V podstatě jsi úlohu na extrém s vazbou převedl na úlohu o extrému funkce jedné proměnné,
což je v pořádku. Že funkce 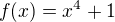 má v bodě 0 lokální (dokonce absolutní) minimum,
má v bodě 0 lokální (dokonce absolutní) minimum,
je zřejmé (neboť pro reálné  je
je 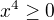 ).
).
Offline
#3 05. 01. 2019 11:16
Re: Vázané extrémy funkce dvou proměnných
↑ Rumburak: děkuji za odpověď.
Mohu poprosit ještě o dovysvětlení, popřípadě o radu, kde bych se to mohl doučit? Mám naučený jen postup, kdy u dosazovací metody lokální extrém je v případě, že právě ta druhá derivace je buď větší, nebo menší než 0.
Offline
#4 05. 01. 2019 12:11
Re: Vázané extrémy funkce dvou proměnných
↑ AterCZ:
Je to spíše o úvaze než o nějaké "metodě".
Když má funkce jedné proměnné na nějakém otevřeném intervalu kladnou první derivaci, je na tomto
intervalu rostoucí, což plyne z předpisu definujícího první derivaci.
Analogicky: Když má funkce jedné proměnné na nějakém otevřeném intervalu zápornou první derivaci,
je na tomto intervalu klesající.
(Obrácená implikace ale neplatí: Je-li funkce na ot. intervalu monotonní, má sice v mnoha jeho bodech
derivaci, ale ne nutně ve všech. )
Odtud plyne i nutná podmínka pro extrém: Ma-li funkce jedné proměnné ve vnitřním bodě intervalu lokální
extrém a zároveň derivaci, je tato rovna nule. Tuto podmínku nelze obrátit - samotná nulovost první derivace
extrém nezajišťuje.
Dále:
Když má funkce jedné proměnné na nějakém otevřeném intervalu kladnou druhou derivaci, je na tomto
intervalu konvexní (její první derivace je rostoucí).
Analogicky: Když má funkce jedné proměnné na nějakém otevřeném intervalu zápornou druhou derivaci,
je na tomto intervalu konkávní (její první derivace je klesající).
Uvedené implikace lze využít při vyšetřování průběhu funkce, ale nelze je obrátit.
Klasickou českou učebnicí na toto téma je Diferenciální počet I od Vojtěcha Jarníka.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vázané extrémy funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)
