Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivace - věta - jednoduchý důkaz (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 01. 2019 18:15
Derivace - věta - jednoduchý důkaz
Ahoj, koukám teď na důkaz jedné věty a nejsem si tím moc jistý.
Věta: Jestliže je derivace f'(x0) konečná, pak je funkce f spojitá v bodě x0.
1) lim (f(x0 + h) - f(x0)) = ... = 0 kde h->0
Nemůžeme ihned rozhodnout, že tato limita je rovna nule, neboť nevíme, zda f(x0) je číslo (konečné)? Proto to děláme přes tu derivaci, neboť víme, že ta konečná je?
2) lim (f(x0 + h) - f(x0)) = 0 <=> lim f(x0 + h) = lim f(x0) = f(x0) kde h->0
Znamená limita v x0 je rovna funkční hodnotě v x0?
Offline
- (téma jako vyřešené označil(a) Kleanthés)
#3 05. 01. 2019 18:52
Re: Derivace - věta - jednoduchý důkaz
↑ Kleanthés: Este k tvojej hypoteze “neboť nevíme, zda f(x0) je číslo (konečné)?“
Vobec nie, vieme to velmi dobre. Ak predpokladame existenciu derivacie funkcie  v bode, musi byt
v bode, musi byt  v tomto bode definovana.
v tomto bode definovana.
Offline
#4 05. 01. 2019 19:09 — Editoval Kleanthés (05. 01. 2019 19:10)
Re: Derivace - věta - jednoduchý důkaz
↑ jarrro:
Dobře, funkce zobrazuje číslo na číslo, tedy f(x0) je také číslo. Potom ale f(x0) - f(x0) = 0 a vidíme rovnou, že 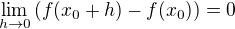 , ne?
, ne?
Takže proč je tam ta derivace? Z toho mi vyplývá, že ta derivace musí být konečná... A z toho zase ta spojitost...
Hele teď mi to začíná dávat smysl, když se na ten důkaz dívám zprava doleva.
Offline
#5 05. 01. 2019 19:11
Re: Derivace - věta - jednoduchý důkaz
↑ vlado_bb:Tak tak, předtím jsem se do toho nějak zamotal. :D
Offline
#6 06. 01. 2019 16:00 — Editoval jarrro (06. 01. 2019 16:01)
Re: Derivace - věta - jednoduchý důkaz
↑ Kleanthés:
Pri nekonečnej derivácii môže byť aj nespojitosť.
Napr. keď 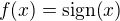 , tak
, tak
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivace - věta - jednoduchý důkaz (TOTO TÉMA JE VYŘEŠENÉ)

 je pevne zvolené číslo z definičného oboru (lebo sa predpokladá existencia derivácie) teda aj
je pevne zvolené číslo z definičného oboru (lebo sa predpokladá existencia derivácie) teda aj 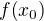 je reálne číslo.
je reálne číslo.