Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Pravděpodobnost 4 karet při tahání 5 karet.
#1 07. 01. 2019 20:16
Pravděpodobnost 4 karet při tahání 5 karet.
Ahoj, zadání je máme balíček 32 karet a taháme jich 5. Jaká je pravděpodobnost, že vytáhneme 2 kluky a 2 desítky?
Já vždy počítám počet "správných" jevů ku počtu všech jevů  .
.
No a počet možností jak namíchat 2 kluky je  , u desítek to samé, mezi sebou to je
, u desítek to samé, mezi sebou to je  .
.
Pátá karta může být jedna z 28, takže 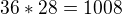 . Zbylých 27 karet má
. Zbylých 27 karet má  kombinací a ještě našich prvních 5 karet můžeme zamíchat mezi sebou
kombinací a ještě našich prvních 5 karet můžeme zamíchat mezi sebou 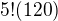 způsoby. Takže výsledek by byl
způsoby. Takže výsledek by byl  ale vím, že to je špatně. Mám dneska po zkoušce z jiného předmětu a ne a ne přijít na správné řešení.. díky
ale vím, že to je špatně. Mám dneska po zkoušce z jiného předmětu a ne a ne přijít na správné řešení.. díky
Offline
#3 07. 01. 2019 20:40
Re: Pravděpodobnost 4 karet při tahání 5 karet.
↑ zdenek1: No jde mi o to, že když označím kluky J a desítky D, barvy čísly 1234, tak když budu táhnout řekněme J1, D2, J2, D3 a pátá karta bude J4, tak když budu táhnout J1,D2,J4,D3 a pátá bude J2, tak tahle možnost je tam 2x, ne? Já to překombinoval, protože já počítám poměr VŠECH namíchání, ne jen poměr kombinací.
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Pravděpodobnost 4 karet při tahání 5 karet.

