Matematické Fórum

Proch · 17. 01. 2019 23:45

Prosím o pomoc s jedním příkladem z Petákovky (str102/44/a)

Jsou dány body $M[3; -2\sqrt{2}], N[-1; 2\sqrt{2}]$ . Určete Souřadnice bodu O tak, aby trojúhelník MNO byl pravoúhlý a rovnoramenný, s pravým úhlem u vrcholu M.

Skoušel jsem to počítat.
O=[x; y]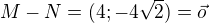
$M-N=(4; -4\sqrt{2})=\vec{o}$
$M-O=(3-x; -2\sqrt{2}-y)=\vec{n}$

Potřebuji dostat soustavu rovnic použiju tedy rovnici pro kolmost MO na MN
Po dosazení: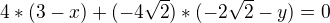
$4*(3-x)+(-4\sqrt{2})*(-2\sqrt{2}-y)=0$

Jako druhou jsem použil rovnici porovnání MO=MN jelikož je trojúhelník rovnoramenný
Po dosazení:
$\sqrt{(3-x)^{2}+(-2\sqrt{2}-y)^{2}}=\sqrt{4^{2}+(-4\sqrt{2})^{2}}$

Vytknul jsem si x z první rovnice: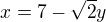
$x=7-\sqrt{2}y$

Ale následný výpočet mi už nevyšel
Děkuji za pomoc. Nevím jestli mám chybu ve rovnicích nebo v následných úpravách, ale už opravdu nevím co s tím.

laszky · 18. 01. 2019 00:57

↑ Proch:

Ahoj. $x=7+\sqrt{2}y$

Proch · 18. 01. 2019 07:21

Děkuji jednalo se vskutku jen o mou hloupost.

Matematické Fórum

#1 17. 01. 2019 23:45

Kolmost vektorů

#2 18. 01. 2019 00:57

Re: Kolmost vektorů

#3 18. 01. 2019 07:21

Re: Kolmost vektorů

Zápatí