Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Fyzika
- » Magnetické pole generované dodatečným proudem (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 01. 2019 05:05
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Magnetické pole generované dodatečným proudem
Fork ↑↑ tohoto: vlákna:
Pokud budeme například nabíjet kondenzátor (třeba deskový, nebo dvě koule vedle sebe) konstantním proudem, nikdo na světě nemůže tvrdit, že pole mezi elektrodami je konstantní (statické). Ne - bude se v čase lineárně zvětšovat. To možná vyvolá nějaké magnetické pole (ve skutečnosti né, ale to je na jinou kapitolu)



Podle rovnice (11.13) (na 3. stránce) mi připadá, že magnetické pole vytvářejí i posuvný a vázaný proud, nejen proud  ?
?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
- (téma jako vyřešené označil(a) KennyMcCormick)
#2 18. 01. 2019 10:38
Re: Magnetické pole generované dodatečným proudem
Někde tady:
https://web.archive.org/web/20150111095 … 8bdc10e975
je velmi dlouhé vlákno, které se myslím jmenuje "posuvný proud ve vakuu"
Offline
#3 19. 01. 2019 04:17
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Našel jsem to vlákno, ale je tam archivovaná jenom první strana, na které je jeden argument proti posuvnému proudu generujícímu magnetické pole:
Magnetické pole vytvářené posuvným proudem dE/dt je ve skutečnosti úplně stejné, jako mag. pole vytvářené normálním proudem j. Takže mezi deskami kondenzátoru bude přesně takové magnetické pole, jako by tam místo dielektrika byl vodič a proud (normální) jím protékal.
S tím souhlasím. Ale na to není nutné, aby Maxwellův proud generoval magnetické pole.
Ale na to by bylo potřeba najít chybu v tom naskenovaném odvození. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#4 19. 01. 2019 09:36
Re: Magnetické pole generované dodatečným proudem
Takže bude další 10-stránková diskuse ?
Ono je jinak dost ošidné, pokud používáme rovnice pole, se ptát na to, co vlastně pole vytváří. Ale zhruba jde o tohle:
(Ale nejdřív si napíšeme "správné" Maxwellky, co neobsahují žádný balast jako je D a H)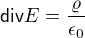
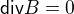
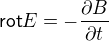
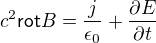
Offline
#5 19. 01. 2019 09:49
Re: Magnetické pole generované dodatečným proudem
Pokud tedy budeme uvažovat jen případy s konstantním proudem a konstantním E, tak z poslední rovnice zbude jen 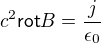
Tahle rovnice nám ovšem sama pole B neurčuje, takže nemůžeme jednoduše tvrdit, že kde je proud, je i magnetické pole. Ovšem po úpravě dostaneme: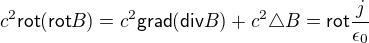
Z jiné rovnice plyne, že div B = 0, takže první člen je nulový, takže dostáváme: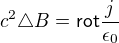
To už je známá Poissonova rovnice, podle které pole spočítat dokážeme - a jeho "zdroj" je veličina rot j.
To je celé. Teď se zbývá zamyslet nad tím, kdy je rot j nulová a kdy není. Například víme, že homogenní vektorové pole má rotaci nulovou. Takže konstantní proud protékající celým prostorem nám žádné magnetické pole nevytvoří. Pokud proud necháme protékat běžným drátem, zjistíme, že nenulovou (dokonce asi nekonečnou) rotaci má jen na hranicích toho vodiče. Uvnitř (za ideálních podmínek homogenního rozložení proudu) žádná rotace není. Venku taky né (když tam žádný proud neteče).
Takže můžeme s trochou nadsázky říct, že za magnetické pole nemůže ten proud, ale to, je je v prostoru ohraničený.
Offline
#6 19. 01. 2019 09:56
Re: Magnetické pole generované dodatečným proudem
Tím jsme se dostali už skoro nakonec. Pokud necháme proud protékat mezi dvěma elektrodami prostředím, které je vodivé (dvě kuličky někde v hlubokém moři, např), a budeme předpokládat, že platí Ohmův zákon, tedy 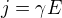 , tak rozložení proudového pole je stejné jako rozložení elektrického pole. A to lze (zase za podmínky, že se nemění B) popsat pomocí potenciálu
, tak rozložení proudového pole je stejné jako rozložení elektrického pole. A to lze (zase za podmínky, že se nemění B) popsat pomocí potenciálu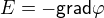
kde potenciál splňuje Laplaceovu rovnici.
A potenciální pole má nulovou rotaci - to je identita z vektorové analýzy, že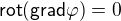
A když nemá rotaci E, nebude ji tedy mít ani j (zase, za předpokladu, že  je konstantní v celém prostoru). A když nemá j rotaci, nevytváří příspěvek k magnetickému poli (viz předchozí příspěvky).
je konstantní v celém prostoru). A když nemá j rotaci, nevytváří příspěvek k magnetickému poli (viz předchozí příspěvky).
U proudového pole není ovšem problém zařídit, aby rotaci mělo, protože není problém zařídit, aby  konstantní nebylo (stačí vodič obalit kouskem "vzduchu"). Takže je to spíš taková rarita.
konstantní nebylo (stačí vodič obalit kouskem "vzduchu"). Takže je to spíš taková rarita.
Offline
#7 19. 01. 2019 10:05 — Editoval MichalAld (19. 01. 2019 10:05)
Re: Magnetické pole generované dodatečným proudem
Jiná situace je ovšem u posuvného proudu 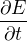
Úplně stejnou hru, jako jsme hráli s konvenčním proudem můžeme hrát i s posuvným. Takže dojdeme k tomu, že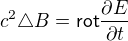
Jenže tady už nic nevymyslíme. Není tu žádná konstanta (jako byla ta vodivost u proudu), jejíž nehomogenitou bychom mohli rotaci vytvořit. Tady máme prostě (pro spojité funkce):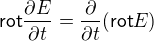
a z Maxwellových rovnic víme, že: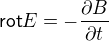
Pokud bude B konstantní v čase, tak bude rotace posuvného proudu nulová a jeho příspěvek k magnetickému poli taky. Můžeme (posuvný proud) klidně vynechat a vypočtené pole bude úplně stejné.
Offline
#8 19. 01. 2019 10:09
Re: Magnetické pole generované dodatečným proudem
Je to takové docela zvláštní - a nikde jsem se s takovouto argumentací nesetkal. Je to vlastně z mojí hlavy - kdysi na Aldebaranu to někdo tvrdil, že posuvný proud magnetické pole nevytváří, a já se snažil dokázat opak tak dlouho, až jsem došel k tomuhle odvození.
Přijde mi to celkem průhledné, ale jak říkám, je to z mojí hlavy, a ani můj hrdina Feynman se o ničem takovém nikde nezmiňuje. Naopak se všude píše, jak posuvný proud má stejné magnetické účinky jako ten obyčejný. Ale nikde už se nepíše, že posuvný proud nedokážeme v prostoru nijak "natvarovat" - jako to běžně děláme s obyčejným proudem - a že když ho "vhodně nenatvarujeme", tak nám žádné magnetické pole nevytvoří.
Offline
#9 19. 01. 2019 12:46 — Editoval LukasM (19. 01. 2019 12:59)
Re: Magnetické pole generované dodatečným proudem
MichalAld napsal(a):
Teď se zbývá zamyslet nad tím, kdy je rot j nulová a kdy není. Například víme, že homogenní vektorové pole má rotaci nulovou. Takže konstantní proud protékající celým prostorem nám žádné magnetické pole nevytvoří.
Tohle je nějaké divoké. Tvá rovnice (ve které je navíc špatně znaménko, ale to je detail) vůbec neříká, že při nulové 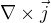 je magnetické pole nulové. Říká maximálně tak to, že jakási kombinace jeho druhých prostorových derivací má být nulová. Mnoho nenulových polí toto bez problémů splní - např. pole tvaru
je magnetické pole nulové. Říká maximálně tak to, že jakási kombinace jeho druhých prostorových derivací má být nulová. Mnoho nenulových polí toto bez problémů splní - např. pole tvaru 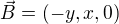 , které bys právě našel uvnitř toho vodiče s homogenním proudem. To mimochodem plyne přímo z jedné tvé výchozí rovnice (Ampérova zákona), se kterou jsi ve sporu. Ano, až bude homogenní hustota proudu v celém prostoru, nikde nebude magnetické pole. Ale to bude mít ten prostý důvod, že se pole od všech proudů vyruší.
, které bys právě našel uvnitř toho vodiče s homogenním proudem. To mimochodem plyne přímo z jedné tvé výchozí rovnice (Ampérova zákona), se kterou jsi ve sporu. Ano, až bude homogenní hustota proudu v celém prostoru, nikde nebude magnetické pole. Ale to bude mít ten prostý důvod, že se pole od všech proudů vyruší.
Vzhledem k tomu, že na tomto stojí celá argumentace se mi zdá, že vyvracíš něco jiného, než si myslíš.
Offline
#10 19. 01. 2019 14:34 — Editoval MichalAld (19. 01. 2019 14:36)
Re: Magnetické pole generované dodatečným proudem
LukasM napsal(a):
Říká maximálně tak to, že jakási kombinace jeho druhých prostorových derivací má být nulová. Mnoho nenulových polí toto bez problémů splní - např. pole tvaru
, které bys právě našel uvnitř toho vodiče s homogenním proudem.
Ta "jakási kombinace druhých derivací" se samozřejmě jmenuje Laplaceova rovnice, případně Poissonova rovnice, když má nenulovou pravou stranu.
A to je právě taková ta zvláštní věc - Laplaceovu rovnici splňuje samozřejmě velké množství funkcí - je to nakonec jedna z nejpoužívanějších rovnic ve fyzice, takže i ta funkce co zmiňuješ ji samozřejmě splňuje. Všechny tyhle funkce mají ale jednu společnou vlastnost - někde nám vždycky utečou do nekonečna. A jako takové je tudíž musíme označit za nefyzikální.
Jediná funkce, co Laplaceovu rovnici splňuje v celém prostoru a přitom do nekonečna nikde neutíká, je konstanta. A konstantní pole v celém prostoru také za fyzikální případ asi považovat nebudeme.
Pokud tedy po řešení požadujeme, aby v nekonečné vzdálenosti mělo nulovou hodnotu (to je takový intuitivní požadavek), a ještě chceme, aby funkce v celém prostoru existovala, má to jediné řešení - nulové v celém prostoru.
(když si vzpomeneme, jak se Laplaceova rovnice v praxi používá - třeba při výpočtu teploty uvnitř tělesa - vždy máme zadané okrajové podmínky. Nikdy nepočítáme celý prostor).
Poissonova rovnice (s pravou stranou) naproti tomu dokáže dát netriviální řešení takové, aby v nekonečnu kleslo na nulu. Dokonce ho lze napsat analyticky, pomocí metody Greenových funkcí. Což znamená, že pravou stranu nahradíme součtem navzájem posunutých Diraců, a ke každému získáme "posunuté řešení" (běžně známé jako potenciál bodového náboje). Proto můžeme říct, že Poissonova rovnice nám pole určuje - a každý bod, kde je pravá strana nenulová, nám tvoří příspěvek k celkovému řešení.
A ta nefyzikální (divergující) řešení jsme vyloučili volbou okrajové podmínky (nulová hodnota v nekonečné vzdálenosti) a požadavkem na spojitost (či existenci) řešení v celém prostoru.
Takže i tvůj příklad magnetického pole nemůže platit v celém prostoru, takové pole by nebylo fyzikální. Může platit jen uvnitř nějakých okrajových podmínek. Aniž se přitom staráme, co tyto podmínky fyzikálně vytvořilo.
Pokud tedy pravá strana rovnice je v celém prostoru nulová (a existující), nemá tato rovnice žádné fyzikální řešení, krom nulového.
Offline
#11 19. 01. 2019 14:48
Re: Magnetické pole generované dodatečným proudem
LukasM napsal(a):
které bys právě našel uvnitř toho vodiče s homogenním proudem. To mimochodem plyne přímo z jedné tvé výchozí rovnice (Ampérova zákona), se kterou jsi ve sporu. Ano, až bude homogenní hustota proudu v celém prostoru, nikde nebude magnetické pole. Ale to bude mít ten prostý důvod, že se pole od všech proudů vyruší.
Tohle je taky taková zvláštní věc - když budeme mít homogenní proudové pole přes celý prostor, a pokusíme se v něm aplikovat Ampérův zákon, narazíme na problémy.
Zvolíme si nějakou osu, ve směru proudu - a aplikujeme Ampérův zákon, tak jak jej známe .... vyplyne nám z toho, že podél kružnice musí (alespoň někde) být nenulové magnetické pole. A čím větší kružnice, tím větší proud jí protéká, tím větší pole by mělo být po jeho obvodu.
No jo, ale když si zvolíme osu o kus vedle, vyjde nám to samé, ale někde jinde.
Nakonec dojdeme k tomu, že nemáme nejmenší tušení, jak by takové magnetické pole mělo vypadat, aby splňovalo Ampérův zákon pro všechny možné osy, co si v prostoru zvolíme.
Ampérův zákon tedy nemůže mít takovou úplně neomezenou platnost, někde jsme nesplnili nějakou podmínku (ale já po pravdě úplně přesně nevím jakou).
Offline
#13 19. 01. 2019 18:20
Re: Magnetické pole generované dodatečným proudem
↑ MichalAld:
"Mé" magnetické pole ani nemělo existovat v celém prostoru, měl to být pouze protipříklad k tvrzení "kde je nulová rotace 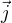 , tam není magnetické pole". Ale jak vidím, tak takhle primitivně jsi to nemyslel.
, tam není magnetické pole". Ale jak vidím, tak takhle primitivně jsi to nemyslel.
Stále se mi to ale nelíbí. Tvá snaha aplikovat jednu rovnici na celý prostor, který je dle předpokladu přesně homogenní podle mně způsobila zanedbání důležité věci, a to sice že pokud "všude" teče proud stejným směrem a nic jiného tam není, tak tam také není nic, co by udržovalo to konstantní elektrické pole. A protože náboje tečou jedním směrem, pole konstantní nezůstane a nebylo správně tu časovou derivaci zanedbat. Výsledek pak předpokládám bude takový, že tam žádné pole nebude, protože vliv vodivostního a Maxwellova proudu se zruší (jako v příkladech v FP 2, 18.2).
Navíc se mi teda zdá dost bizardní předpokládat homogenní prostor plný proudu bez jakýchkoli okrajů, a zároveň "intuitivně" čekat, že tam něco bude směrem ven klesat k nule. Tento intuitivní předpoklad je pro mně intuitivní jen v případě, že se vše zajímavé v tom prostoru dá zavřít do (konečné) krabice, vně které už nic není.
Pokud jde o ty problémy s Ampérovým zákonem, neviděl bych to tak tragicky. Mluvíš o nějakých kružnicích, takže asi používáš Ampérův zákon v integrálním tvaru. Ten ale nevrací pole v daném bodě, ale jen tu část vytvořenou proudy uvnitř té kružnice (resp. jen jeho integrál podél té kružnice). Tam žádný problém nevidím.
Vlastně mi celkově nějak není jasné, o co tu má jít. Hustota Maxwellova proudu (polarizační proudy zanedbám) je definována jako 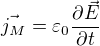 . Tohle je druhý člen v rovnici pro
. Tohle je druhý člen v rovnici pro 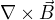 a musí to tedy být stejně dobrý zdroj magnetického pole jako "obyčejný" vodivostní proud. Nějak v tom nevidím prostor pro žádné kroky stranou. Pokud tím zázrakem má být "Pokud bude B konstantní v čase, tak bude rotace posuvného proudu nulová a jeho příspěvek k magnetickému poli taky.", tak se mi tak trochu zdá, že ten případ "B konstatní v čase, někde teče nenulový Maxwellův proud a současně je jeho rotace všude nulová" prostě neexistuje, protože by nesplňoval Maxwellovy rovnice. Ale nepřemýšlel jsem o tom dlouho.
a musí to tedy být stejně dobrý zdroj magnetického pole jako "obyčejný" vodivostní proud. Nějak v tom nevidím prostor pro žádné kroky stranou. Pokud tím zázrakem má být "Pokud bude B konstantní v čase, tak bude rotace posuvného proudu nulová a jeho příspěvek k magnetickému poli taky.", tak se mi tak trochu zdá, že ten případ "B konstatní v čase, někde teče nenulový Maxwellův proud a současně je jeho rotace všude nulová" prostě neexistuje, protože by nesplňoval Maxwellovy rovnice. Ale nepřemýšlel jsem o tom dlouho.
Ani já netvrdím, že tomu dokonale rozumím.
Offline
#14 20. 01. 2019 11:06 — Editoval MichalAld (20. 01. 2019 11:11)
Re: Magnetické pole generované dodatečným proudem
LukasM napsal(a):
Vlastně mi celkově nějak není jasné, o co tu má jít. Hustota Maxwellova proudu (polarizační proudy zanedbám) je definována jako
. Tohle je druhý člen v rovnici pro
a musí to tedy být stejně dobrý zdroj magnetického pole jako "obyčejný" vodivostní proud. Nějak v tom nevidím prostor pro žádné kroky stranou. Pokud tím zázrakem má být "Pokud bude B konstantní v čase, tak bude rotace posuvného proudu nulová a jeho příspěvek k magnetickému poli taky.", tak se mi tak trochu zdá, že ten případ "B konstatní v čase, někde teče nenulový Maxwellův proud a současně je jeho rotace všude nulová" prostě neexistuje, protože by nesplňoval Maxwellovy rovnice. Ale nepřemýšlel jsem o tom dlouho.
Problém se dá demonstrovat na zcela konkrétním příkladu. Představ si, že máš vodič ve tvaru prstence, relativně velký (průměr třeba několik metrů, a průměr vodiče několik milimetrů). V jednom místě je do vodiče "vložen" zdroj konstantního proudu (nějaká malá krabička, obsahující svůj vlastní akumulátor a elektroniku kolem, nebo třeba i něco jiného, je to jedno - jen to musí být malé, abychom to nemuseli brát v potaz při počítání). A na druhé straně bude prstencový vodič přerušen nějakou mezerou. Otázka je jak velkou, uvažujme pro začátek srovnatelnou s průměrem vodiče, tedy zase pár milimetrů.
Vodičem tedy teče konstantní proud (o to se stará jeho zdroj), ta mezera je vlastně kondenzátor, který se tím proudem nabíjí a někde v té mezeře a kolem ní "teče" ten Maxwellův posuvný proud.
A teď, chceme spočítat magnetické pole v prostoru kolem tohoto prstence. Proud je konstantní, takže pole B bude také konstantní, takže žádné indukované napětí nám tam nikde nevzniká.
A otázka je - musíme do výpočtu B zahrnout i ten posuvný proud, pocházející z 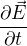 ? A nebo se nic nestane, když jej do výpočtu nezahrneme, protože žádný příspěvek k magnetickému poli nevytvoří ?
? A nebo se nic nestane, když jej do výpočtu nezahrneme, protože žádný příspěvek k magnetickému poli nevytvoří ?
Matematicky zcela ekvivalentní problém dostaneme, pokud celý prstenec umístíme do nějakého vodivého prostředí (hodíme do moře). Potom už tou mezerou a jejím okolím neteče posuvný proud, ale normální proud - jeho rozložení je však úplně stejné. A zase se můžeme ptát - vytváří tento proud (co teče vodivým prostředím mezi elektrodami) nějaký příspěvek k celkovému magnetickému poli, nebo né ?
A to je to, co se snažím dokázat, že nevytváří. Né proto, že by element proudu nevytvářel element magnetického pole, ale proto, že rozložení proudu (ať už posuvného či normálního) je vždy přesně takové, že se jednotlivé příspěvky navzájem vyruší.
Offline
#15 20. 01. 2019 11:10
Re: Magnetické pole generované dodatečným proudem
Ono se jinak rozložení magnetického pole počítá docela blbě, a analyticky tohle s nevětší pravděpodobností vůbec nepůjde řešit, a na simulaci takovýchto úloh nemám žádné dostupné prostředky.
Navíc je to celé složitější než to vypadá - protože celou délkou vodiče neteče konstantní proud, směrem k jeho konci (mezeře) se proud postupně zmenšuje až na nulu (a náboje se postupně ukládají na povrchu vodiče, nebo vytékají do okolního vodivého prostředí). A abychom tohle dokázali spočítat, museli bychom si zřejmě nejprve spočítat rozložení elektrického pole kolem vodičů.
Offline
#16 03. 02. 2019 03:26 — Editoval KennyMcCormick (03. 02. 2019 05:24)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Teď se zbývá zamyslet nad tím, kdy je rot j nulová a kdy není. Například víme, že homogenní vektorové pole má rotaci nulovou.
Pokud je i konstanta řešením, tak z toho neplyne, že posuvný proud v prostoru přispívá k 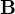 nulovou mírou. Protože právě tak můžeme tvrdit, že přispívá konstantou, což je právě to
nulovou mírou. Protože právě tak můžeme tvrdit, že přispívá konstantou, což je právě to 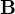 mezi deskami nabíjeného/vybíjeného kondenzátoru (pokud jsem správně pochopil učebnici).
mezi deskami nabíjeného/vybíjeného kondenzátoru (pokud jsem správně pochopil učebnici).
Taky, pokud jsem to správně pochopil, tak 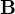 vyvolané posuvným proudem (v učebnici tam ještě připočítávají vázaný proud, ale ten jsi zahrnul do
vyvolané posuvným proudem (v učebnici tam ještě připočítávají vázaný proud, ale ten jsi zahrnul do 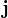 , takže o tom mluvit nemusíme) je právě totéž pole, které se mezi deskami kondenzátoru nachází. Není to nějaký dodatečný příspěvek.
, takže o tom mluvit nemusíme) je právě totéž pole, které se mezi deskami kondenzátoru nachází. Není to nějaký dodatečný příspěvek.
↑ LukasM:
Stále se mi to ale nelíbí. Tvá snaha aplikovat jednu rovnici na celý prostor, který je dle předpokladu přesně homogenní podle mně způsobila zanedbání důležité věci, a to sice že pokud "všude" teče proud stejným směrem a nic jiného tam není, tak tam také není nic, co by udržovalo to konstantní elektrické pole. A protože náboje tečou jedním směrem, pole konstantní nezůstane a nebylo správně tu časovou derivaci zanedbat. Výsledek pak předpokládám bude takový, že tam žádné pole nebude, protože vliv vodivostního a Maxwellova proudu se zruší (jako v příkladech v FP 2, 18.2).
(...)
Pokud jde o ty problémy s Ampérovým zákonem, neviděl bych to tak tragicky. Mluvíš o nějakých kružnicích, takže asi používáš Ampérův zákon v integrálním tvaru. Ten ale nevrací pole v daném bodě, ale jen tu část vytvořenou proudy uvnitř té kružnice (resp. jen jeho integrál podél té kružnice). Tam žádný problém nevidím.
Tohle je zajímavé, protože v celém prostoru vyplněného konstantním 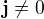 se zdá, jako kdyby muselo být nutně
se zdá, jako kdyby muselo být nutně 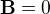 (kvůli symetrii - magnetické pole vyvolané každým elementárním proudem se navzájem zruší).
(kvůli symetrii - magnetické pole vyvolané každým elementárním proudem se navzájem zruší).
Jenže to by protiřečilo Ampérovu zákonu, jak píše ↑ MichalAld:. Ale Ampérův zákon (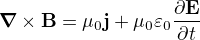 ) je Maxwellova rovnice a musí tedy platit v celém klasickém elektromagnetismu.
) je Maxwellova rovnice a musí tedy platit v celém klasickém elektromagnetismu.
(Nemůžeme použít Ampérův zákon, jako kdyby to byl nekonečně dlouhý válcový vodič s nekonečným poloměrem, protože zatímco takový systém má 1 osu souměrnosti, skutečný nekonečný prostor má nekonečně mnoho os souměrnosti - každá přímka ve směru 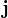 . Výsledek záleží tedy na tom, jakou limitu k definování našeho nekonečného prostoru použijeme - pokud víme pouze to, že je to nekonečný prostor, nemůžeme Ampérův zákon použít. (Btw, Ampérův zákon vrací celé
. Výsledek záleží tedy na tom, jakou limitu k definování našeho nekonečného prostoru použijeme - pokud víme pouze to, že je to nekonečný prostor, nemůžeme Ampérův zákon použít. (Btw, Ampérův zákon vrací celé 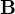 (resp. v případě integrální verze celé
(resp. v případě integrální verze celé 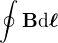 ) - jde o to, že jiný proud, než ten, který plochou určenou danou smyčkou protéká, nemá na
) - jde o to, že jiný proud, než ten, který plochou určenou danou smyčkou protéká, nemá na 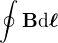 žádný vliv, takže už tam nemusíš nic připočítávat).)
žádný vliv, takže už tam nemusíš nic připočítávat).)
Nakonec jsem zjistil, že je to předpoklad 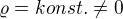 , který je jednak fyzikálně nemožný a jednak nekompatibilní s Maxwellovými rovnicemi. Fyzikálně nemožný je ze zjevného důvodu - náš vesmír takový není. Nekompatibilní s Maxwellovými rovnicemi jednak kvůli Ampérovu zákonu, a jednak např. i kvůli Gaussovu zákonu (
, který je jednak fyzikálně nemožný a jednak nekompatibilní s Maxwellovými rovnicemi. Fyzikálně nemožný je ze zjevného důvodu - náš vesmír takový není. Nekompatibilní s Maxwellovými rovnicemi jednak kvůli Ampérovu zákonu, a jednak např. i kvůli Gaussovu zákonu (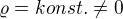 implikuje nulové
implikuje nulové 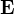 v každém bodě kvůli symetrii, ale každá uzavřená plocha uzavírá nenulový náboj, takže Gaussův zákon by vedl na kontradikci).
v každém bodě kvůli symetrii, ale každá uzavřená plocha uzavírá nenulový náboj, takže Gaussův zákon by vedl na kontradikci).
Ampérův zákon tedy platí vždycky a je to hypotetická situace s konstantním 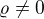 vyplňujícím celý prostor, která je fyzikálně nemožná, tj. i konstantní
vyplňujícím celý prostor, která je fyzikálně nemožná, tj. i konstantní 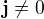 v celém prostoru je fyzikálně nemožné.
v celém prostoru je fyzikálně nemožné.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#17 03. 02. 2019 12:47 — Editoval MichalAld (03. 02. 2019 12:50)
Re: Magnetické pole generované dodatečným proudem
↑ KennyMcCormick:
Že je nutné pole konstantního j v celém prostoru zavrhnout jako nefyzikální, v tom se asi shodneme. Mě to tak taky přijde - protože proud prostě přenáší náboj, a náboj vytváří el. pole.
KennyMcCormick napsal(a):
Teď se zbývá zamyslet nad tím, kdy je rot j nulová a kdy není. Například víme, že homogenní vektorové pole má rotaci nulovou.
Pokud je i konstanta řešením, tak z toho neplyne, že posuvný proud v prostoru přispívá k
nulovou mírou. Protože právě tak můžeme tvrdit, že přispívá konstantou, což je právě to
mezi deskami nabíjeného/vybíjeného kondenzátoru (pokud jsem správně pochopil učebnici).
Taky, pokud jsem to správně pochopil, takvyvolané posuvným proudem (v učebnici tam ještě připočítávají vázaný proud, ale ten jsi zahrnul do
, takže o tom mluvit nemusíme) je právě totéž pole, které se mezi deskami kondenzátoru nachází. Není to nějaký dodatečný příspěvek.
Tohle by bylo dobré, kdybys popsal matematicky, já tomu moc nerozumím.
Když jsem zmiňoval, že konstatnní B je řešením, měl jsem na mysli B konstatní v celém prostoru, né jen "někde". A to určitě není to, co máš na mysli. Přijde mi, že mluvíš zase o Ampérovu zákonu, ale jistý si nejsem.
Z toho co píšeš tak nějak plyne, že pole někde (mezi deskami) je určeno jen proudem tamtéž (mezi deskami). Jenže tak to není. Každý element proudu (ať už normálního, nebo toho posuvného) vytváří příspěvek, který zabírá celý prostor. Je to (skoro) stejné, jako el. pole kolem elementu náboje.
Proto tomu úplně nerozumím, co říkáš - a bylo by lepší, kdybys přímo napsal, o jaký vztah jde.
Offline
#18 03. 02. 2019 12:54
Re: Magnetické pole generované dodatečným proudem
Jinak jen taková nesouvisející poznámka - představa 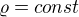 je samozřejmě taky problém, a týká se i gravitace (tam by to nebyla hustota náboje ale "hustota hmotnosti"). Protože Newtonův gravitační zákon je matematicky ekvivalentní Coulombovu zákonu.
je samozřejmě taky problém, a týká se i gravitace (tam by to nebyla hustota náboje ale "hustota hmotnosti"). Protože Newtonův gravitační zákon je matematicky ekvivalentní Coulombovu zákonu.
Zajímavé je, že si s tím nakonec teorie gravitace (OTR) dokázala poradit...
Offline
#19 03. 02. 2019 13:05
Re: Magnetické pole generované dodatečným proudem
Ještě mám v rukávu jeden argument ohledně posuvného proudu - ale teď nemám čas to tu rozvádět.
Jde ale o to, že "správné Maxwelky" nemusejí být ty co obsahují E a B, ale mohou to být ty, co obsahují elektromagnetický potenciál (kvantoví fyzikové určitě zajásají). Ale i v rámci klasické fyziky by měly být navzájem minimálně ekvivalentní.
No a tam (rovnice elektromagnetického potenciálu) žádný posuvný proud (ani jeho ekvivalent) není.
Později to rozepíšu.
Offline
#20 03. 02. 2019 22:34 — Editoval LukasM (04. 02. 2019 00:14)
Re: Magnetické pole generované dodatečným proudem
Ampérův zákon vrací celé
(resp. v případě integrální verze celé
)
Myslel jsem to nejspíš tak, že proudy mimo tu smyčku stále mohou ovlivnit hodnotu samotného pole (proudy uvnitř rozhodují jen o integrálu podél smyčky, jak píšeš). Ale teď jak to čtu podruhé, máš pravdu, že to neřeší Michalův problém (který je zřejmě "tady čekám nulové pole, ale ono má mít nenulovou rotaci").
Ještě jsem o tom prostoru plném proudu chvíli přemýšlel a zdá se mi, že 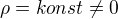 tu nikdo nepředpokládal. Bavili jsme se o případu
tu nikdo nepředpokládal. Bavili jsme se o případu 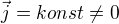 a pokud se nepletu, to může nastat i v případě, že je hustota náboje všude nulová (stačí aby hustota kladných a záporných nábojů byla všude stejná a pohybovaly se na opačnou stranu). Problém zmizí, když nechám proud téct ne v celém prostoru, ale mezi nekonečnými deskami kondenzátoru kolmými na ten proud - pak Ampérův zákon skutečně vrátí mezi deskami
a pokud se nepletu, to může nastat i v případě, že je hustota náboje všude nulová (stačí aby hustota kladných a záporných nábojů byla všude stejná a pohybovaly se na opačnou stranu). Problém zmizí, když nechám proud téct ne v celém prostoru, ale mezi nekonečnými deskami kondenzátoru kolmými na ten proud - pak Ampérův zákon skutečně vrátí mezi deskami 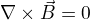 , jak jsem to popsal výše. Ale co je porušeno, když tam ty desky nejsou, to nevím.
, jak jsem to popsal výše. Ale co je porušeno, když tam ty desky nejsou, to nevím.
Edit: Podle mně to musí být ten předpoklad, že tam není elektrické pole. To odnikud neplyne. Elektrické pole bychom museli taky spočítat z Maxwellových rovnic a protože v té naší situaci nemáme rozumné okrajové podmínky, nepůjde dopočítat jednoznačně. Jediné rozumné vysvětlení je, že tam bude narůstat elektrické pole stejně, jako by tam byl ten kondenzátor. Takové pole neporušuje Maxwellovy rovnice a odstraní ten problém. A píšu to šedivě, protože jsem si to právě celé vymyslel.
Do diskuze o posuvném proudu v přerušeném vodiči (nebo co se tu vlastně řeší) se raději přidávat nebudu, tam se mi asi nepodařilo pochopit problém (a ani mi to moc nevadí).
Offline
#21 05. 02. 2019 23:33 — Editoval KennyMcCormick (13. 02. 2019 11:11)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Z toho co píšeš tak nějak plyne, že pole někde (mezi deskami) je určeno jen proudem tamtéž (mezi deskami).
Tak jsem to nemyslel, neboj. 🙂
Když jsem zmiňoval, že konstatní B je řešením, měl jsem na mysli B konstatní v celém prostoru, né jen "někde". A to určitě není to, co máš na mysli.
Aha, tak ne konstanta. B je konstantní v čase, ale ne v prostoru. Nevím, proč jsem to napsal...
Ještě jsi napsal 4 věci:
↑ MichalAld:
1.
Tady máme prostě (pro spojité funkce):
2. Zdrojem magnetického pole je rotace proudové hustoty.
3. Jediným řešením rovnice 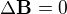 s okrajovou podmínkou
s okrajovou podmínkou 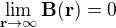 je
je 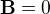 .
.
4. 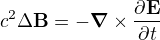 (přidal jsem znaménko mínus).
(přidal jsem znaménko mínus).
Ale:
1. 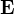 není spojitá, protože ve stěnách hranolu určeného deskami kondenzátoru se skokem mění (minimálně na makroskopické úrovni).
není spojitá, protože ve stěnách hranolu určeného deskami kondenzátoru se skokem mění (minimálně na makroskopické úrovni).
2. Platí 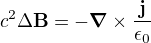 , ale to neznamená, že rotace proudové hustoty vyvolává magnetické pole. Argument Laplaceova operatáru v Poissonově rovnici je potenciál pole, ne pole. Potenciál magnetického pole je
, ale to neznamená, že rotace proudové hustoty vyvolává magnetické pole. Argument Laplaceova operatáru v Poissonově rovnici je potenciál pole, ne pole. Potenciál magnetického pole je  z rovnic
z rovnic  a
a 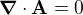 (Edit: ta druhá rovnice neplatí), takže Poissonova rovnice pro magnetické pole je
(Edit: ta druhá rovnice neplatí), takže Poissonova rovnice pro magnetické pole je 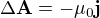 , tj. zdrojem magnetického pole je
, tj. zdrojem magnetického pole je 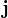 , ne jeho rotace.
, ne jeho rotace.
3. Tohle bys musel dokázat. 🙂
4. Je správně.
↑ MichalAld:
Ale i v rámci klasické fyziky by měly být navzájem minimálně ekvivalentní.
No a tam (rovnice elektromagnetického potenciálu) žádný posuvný proud (ani jeho ekvivalent) není.
V tom případě v rámci klasické fyziky musejí obsahovat ekvivalent posuvného proudu, protože pokud máme dvě fyzikální teorie, které dávají ve všech v principu proveditelných experimentech identické výsledky, pak se tyto dvě teorie liší pouze v sémantice.
Každopádně, pokud existují Maxwellovy rovnice bez posuvného proudu dávájící shodné experimentální výsledky, můžeme se shodnout na tom, že v jedné formulaci posuvný proud vyvolává magnetické pole a ve druhé ne. V takovém případě by to byla jenom otázka sémantiky (pokud se shodneme na všech experimentálních předpovědích).
Btw, rovnice 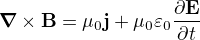 (která platit musí) se dá zapsat i jako
(která platit musí) se dá zapsat i jako 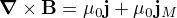 , kde
, kde 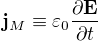 je hustota Maxwellova proudu (která se v tomto případě rovná hustotě posuvného proudu). Takže máme rovnici
je hustota Maxwellova proudu (která se v tomto případě rovná hustotě posuvného proudu). Takže máme rovnici 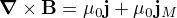 , o které víme, že platí, a její integrální forma je
, o které víme, že platí, a její integrální forma je 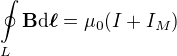 , takže posuvný proud generuje podle Ampérova zákona magnetické pole stejně jako obyčejný proud. (Na těch 3 naskenovaých stranách z prvního příspěvku je to podrobněji.) Takže podle mě je to jenom otázka toho, najít chybu v úvaze, která říká, že to tak není, ať už se chyba nachází kdekoliv.
, takže posuvný proud generuje podle Ampérova zákona magnetické pole stejně jako obyčejný proud. (Na těch 3 naskenovaých stranách z prvního příspěvku je to podrobněji.) Takže podle mě je to jenom otázka toho, najít chybu v úvaze, která říká, že to tak není, ať už se chyba nachází kdekoliv.
↑ LukasM:
Ještě jsem o tom prostoru plném proudu chvíli přemýšlel a zdá se mi, že
tu nikdo nepředpokládal. Bavili jsme se o případu
a pokud se nepletu, to může nastat i v případě, že je hustota náboje všude nulová (stačí aby hustota kladných a záporných nábojů byla všude stejná a pohybovaly se na opačnou stranu).
No jo. Takže fyzikálně nemožný (a nekompatibilní s Maxwellovými rovnicemi) stav je už 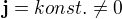 .
.
Problém zmizí, když nechám proud téct ne v celém prostoru, ale mezi nekonečnými deskami kondenzátoru kolmými na ten proud - pak Ampérův zákon skutečně vrátí mezi deskami
, jak jsem to popsal výše.
Tady nevím, co myslíš, resp. proč 0? Mezi deskami nabíjejícího se/vybíjejícího se kondenzátoru není nulová rotace B, a mezi deskami statického kondenzátoru zase není žádný proud. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#22 08. 02. 2019 20:05
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
1.
není spojitá, protože ve stěnách hranolu určeného deskami kondenzátoru se skokem mění (minimálně na makroskopické úrovni).
Ale no tak, všechny věci ve skutečném světě jsou spojité, tyhle nespojitosti jsou jen v našich zjednodušených modelech. Tak si holt představíme rozložení elektronů u povrchu vodiče takové, aby se E měnilo spojitě (elektrony určitě nezabírají nekonečně tenkou vrstvu na povrchu - to jaksi není v reálném světě možné).
KennyMcCormick napsal(a):
2. Platí
, ale to neznamená, že rotace proudové hustoty vyvolává magnetické pole. Argument Laplaceova operatáru v Poissonově rovnici je potenciál pole, ne pole. Potenciál magnetického pole je
z rovnic
a
, takže Poissonova rovnice pro magnetické pole je
, tj. zdrojem magnetického pole je
, ne jeho rotace.
Je otázka, jestli za magnetické pole považujeme pole A, nebo pole B. Mě je to jedno.
Ale na tu rovnici 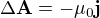 aplikujeme rotaci (na obě strany), a zase, u dostatečně slušných funkcí můžeme operátory prohodit a dostaneme (protože
aplikujeme rotaci (na obě strany), a zase, u dostatečně slušných funkcí můžeme operátory prohodit a dostaneme (protože  ) přímo tu rovnici pro B. To je přece jedno, v jakém se to udělá pořadí.
) přímo tu rovnici pro B. To je přece jedno, v jakém se to udělá pořadí.
KennyMcCormick napsal(a):
3. Tohle bys musel dokázat. 🙂
Časem to dohledám i pro 3D případ. Ve 2D je to známější, protože LaPlaceovu rovnici splňuje každá "slušná" komplexní funkce z = z(x+jy), a pro ně platí Liouvilleova věta - že každá ohraničená holomorfní funkce musí být konstantní. Tedy pokud konstantní není, není ohraničená (utíká do nekonečna, někde).
Nakonec, jsme na matematickém fóru, tak by se toho (důkazu) mohl ujmout někdo z matematiků...
KennyMcCormick napsal(a):
4. Je správně.
Tak to jsem rád, hi...
Offline
#23 08. 02. 2019 20:11
Re: Magnetické pole generované dodatečným proudem
KennyMcCormick napsal(a):
Ale i v rámci klasické fyziky by měly být navzájem minimálně ekvivalentní.
No a tam (rovnice elektromagnetického potenciálu) žádný posuvný proud (ani jeho ekvivalent) není.V tom případě v rámci klasické fyziky musejí obsahovat ekvivalent posuvného proudu, protože pokud máme dvě fyzikální teorie, které dávají ve všech v principu proveditelných experimentech identické výsledky, pak se tyto dvě teorie liší pouze v sémantice.
No ano - a pokud jedny rovnice obsahují posuvný proud jako zdroj B a druhé né, a obojí jsou ekvivalentní - tj předpovíme pomocí nich stejné magnetické pole B, tak je celkem nasnadě, že ten posuvný proud nám žádný příspěvek k B nakonec nevytvoří.
Týká se to samozřejmě jen případu, kdy je posuvný proud konstantní v čase - což je takový dost specifický a v praxi se často nevyskytující případ.
Offline
#24 10. 02. 2019 07:08 — Editoval KennyMcCormick (10. 02. 2019 07:58)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Magnetické pole generované dodatečným proudem
Teď už jsem si ~100% jistý, že mám pravdu. (Ale i tak mě oprav, jestli jsem něco napsal špatně.) 🙂
Ale no tak, všechny věci ve skutečném světě jsou spojité
V našem modelovém systému nejsou spojité. (Např. v místě desek je nedefinované 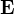 , konstantní
, konstantní 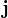 ve vodiči znamená, že
ve vodiči znamená, že 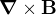 na okraji vodiče je nespojitá, atd.)
na okraji vodiče je nespojitá, atd.)
Edit: Tam by mě zajímalo, jak by se měnila ta hustota náboje na deskách, pokud by výsledné 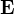 bylo spojité a jak to je v souladu s tím, že se dá ukázat, že náboj bude pouze v nekonečně tenké vrstvě na povrchu. (Možná je nějaká hlubší analýza, která ukazuje, že je to možné, nebo to souvisí s tím, že se elektrické pole mění v čase... (Nemohou to být ale elektrony, protože elektrony představují v klasickém elektromagnetismu nespojitost
bylo spojité a jak to je v souladu s tím, že se dá ukázat, že náboj bude pouze v nekonečně tenké vrstvě na povrchu. (Možná je nějaká hlubší analýza, která ukazuje, že je to možné, nebo to souvisí s tím, že se elektrické pole mění v čase... (Nemohou to být ale elektrony, protože elektrony představují v klasickém elektromagnetismu nespojitost 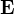 .))
.))
Časem to dohledám i pro 3D případ. Ve 2D je to známější, protože LaPlaceovu rovnici splňuje každá "slušná" komplexní funkce z = z(x+jy), a pro ně platí Liouvilleova věta - že každá ohraničená holomorfní funkce musí být konstantní. Tedy pokud konstantní není, není ohraničená (utíká do nekonečna, někde).
Tady si to můžeme rozdělit na 3 různé případy, o kterých můžeme mluvit. U každého porovnáme Maxwellovy rovnice a tvoje odvození.
1. Konečný deskový kondenzátor s deskami ve tvaru kruhu o poloměru  a vzdáleností
a vzdáleností  mezi deskami (kde
mezi deskami (kde 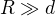 ), osa souměrnosti kondenzátoru je osa x, střed spodní podstavy je v bodě
), osa souměrnosti kondenzátoru je osa x, střed spodní podstavy je v bodě ![kopírovat do textarea $\left[-\frac d2,0,0\right]$](/mathtex/87/87461dbc0bd0dd20639121a8fe1a9544.gif) a střed horní podstavy
a střed horní podstavy ![kopírovat do textarea $\left[\frac d2,0,0\right]$](/mathtex/ed/ed677535f2d95a126bac228dc9a3ca45.gif) . Proud teče v kladném směru osy x.
. Proud teče v kladném směru osy x.
Jak bude magnetické pole mezi deskami vypadat v takovém případě?
Podle Maxwellových rovnic:
Proč není tvoje odvození možné:
2. Limitně nekonečný deskový kondenzátor s deskami ve tvaru kruhu o poloměru
 a vzdáleností
a vzdáleností  mezi deskami (kde
mezi deskami (kde 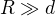 ), osa souměrnosti kondenzátoru je osa x, střed spodní podstavy je v bodě
), osa souměrnosti kondenzátoru je osa x, střed spodní podstavy je v bodě ![kopírovat do textarea $\left[-\frac d2,0,0\right]$](/mathtex/87/87461dbc0bd0dd20639121a8fe1a9544.gif) a střed horní podstavy
a střed horní podstavy ![kopírovat do textarea $\left[\frac d2,0,0\right]$](/mathtex/ed/ed677535f2d95a126bac228dc9a3ca45.gif) . Proud teče v kladném směru osy x, kde
. Proud teče v kladném směru osy x, kde  a
a  necháme jít k nekonečnu (tak, aby zůstala zachována podmínka
necháme jít k nekonečnu (tak, aby zůstala zachována podmínka 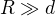 .
.Podle Maxwellových rovnic:
Proč není tvoje odvození možné:
3. Posuvný proud
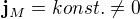 ve skutečně nekonečném prostoru
ve skutečně nekonečném prostoruPodle Maxwellových rovnic:
Proč není tvoje odvození možné:
No ano - a pokud jedny rovnice obsahují posuvný proud jako zdroj B a druhé né, a obojí jsou ekvivalentní - tj předpovíme pomocí nich stejné magnetické pole B, tak je celkem nasnadě, že ten posuvný proud nám žádný příspěvek k B nakonec nevytvoří.
Není to tak. Posuvný proud je součet Maxwellova a polarizačního proudu. Polarizační proud je v našem případě roven nule, takže posuvný proud je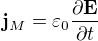 .
.
A intenzita je záporný gradient potenciálu. Takže pokud můžeme popsat změnu intenzity v čase nebo změnu potenciálu v čase, tak tam je implicitně posuvný proud.
Ještě bys to mohl myslet tak, že protože 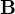 nemůžeme přímo pozorovat, tak můžeš mít dva různé popisy magnetického pole s použitím
nemůžeme přímo pozorovat, tak můžeš mít dva různé popisy magnetického pole s použitím 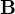 a přesto se shodnout na všech v principu proveditelných experimentálních předpovědích. V tom případě bychom se já a ty lišili jenom v sémantice (protože když dvě různé teorie předvídají všechny fyzikálně realizovatelné experimenty identicky, liší se tyhle dvě teorie jenom v sémantice).
a přesto se shodnout na všech v principu proveditelných experimentálních předpovědích. V tom případě bychom se já a ty lišili jenom v sémantice (protože když dvě různé teorie předvídají všechny fyzikálně realizovatelné experimenty identicky, liší se tyhle dvě teorie jenom v sémantice).
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#25 10. 02. 2019 07:24 Příspěvek uživatele KennyMcCormick byl skryt uživatelem KennyMcCormick.
- Hlavní strana
- » Fyzika
- » Magnetické pole generované dodatečným proudem (TOTO TÉMA JE VYŘEŠENÉ)

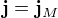 , kde
, kde 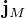 je Maxwellův proud, který se v tomto případě rovná posuvnému proudu (protože tam není žádný polarizační proud, protože mezi deskami je vakuum).
je Maxwellův proud, který se v tomto případě rovná posuvnému proudu (protože tam není žádný polarizační proud, protože mezi deskami je vakuum).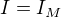 , platí (jak ve vodiči, tak mezi deskami), že magnetické pole je stejné, jako byl tam všude byl jenom vodič s proudem
, platí (jak ve vodiči, tak mezi deskami), že magnetické pole je stejné, jako byl tam všude byl jenom vodič s proudem 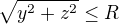 je
je , kde
, kde  je vzdálenost od osy x. Směr
je vzdálenost od osy x. Směr  je
je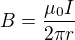 .
.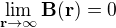 ).)
).)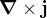 není definovaná v plášti vodiče (musel bys změnit
není definovaná v plášti vodiče (musel bys změnit 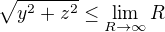 je
je je
je a
a  platí
platí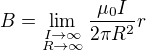 , kde
, kde 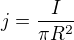 , dostáváme
, dostáváme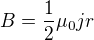 .
. není omezená.
není omezená. všude, neplatila by jedna z Maxwellových rovnic (protože levá strana by se rovnala nule (nulová rotace
všude, neplatila by jedna z Maxwellových rovnic (protože levá strana by se rovnala nule (nulová rotace 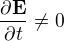 ).
).