Matematické Fórum

Roscelinius · 25. 01. 2019 09:53

Dobrý den,
obracím se na Vás s ujasněním problému složek vektoru.
Díváme li se na vektor jako na objekt n rozměrného vektorového prostoru je nezávislí na volbě báze, jde o kontravariantní tenzor prvního řádu 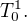$T^{1}_{0}.$

Vektor je reprezentován v konkrétní bázi pomocí složek (vektoru složek, tedy souřadnic) v dané bázi: $\vec{v} = (v)=v^{i} e_{i}$ .
Pokud zavedeme ortonormální standardní bázi můžeme vektor vyjádřit pomocí složek $\vec{v} =v^{i}$ tedy např. v n=3 $\vec{v} =(v^{1},v^{2}, v^{3}).$

Mohu zapsat vektor, tedy objekt vektorového prostoru invariantní na volbě báze, pomocí jeho složek? Složky vektoru jsou dány dimenzí vektorového prostoru, bez ohledu na reprezentaci. Jak mohu v zápise oddělit složky vektoru nezávislého na volbě báze od vektoru složek (souřadnic) v konkrétní bázi?
Děkuji

MichalAld

Nemyslím si, že jde nějak zapsat vektor nezávisle na použité bázi.

Představa vektoru nezávislého na bázi je abstrakce, protože operace, které můžeme s vektory provádět, na volbě báze nezávisí. Přesně řečeno - můžeme vždy nejprve provést operaci a potom změnu báze, nebo nejprve změnu báze a potom operaci. Takže si můžeme představovat abstraktní vektor, jehož vlastnosti na volbě báze nezávisí.

Pokud ovšem chceme dosadit nějaká konkrétní čísla, tak si nějakou bázi zvolit musíme.

Ale je to jen můj názor...

Matematické Fórum

#1 25. 01. 2019 09:53

Složky vektoru

#2 25. 01. 2019 10:09 — Editoval MichalAld (25. 01. 2019 10:13)

Re: Složky vektoru

Zápatí