Matematické Fórum

Davisek · 27. 01. 2019 02:09

Zdravim,

potreboval bych nejakou radu jak dokazat nasledujici tvrzeni:

Necht $A, B$ jsou dve mnoziny, pak
$\Big[x \in A \wedge x \notin B\Big] \vee \Big[x \notin A \wedge x \in B\Big] \iff \Big[x \in (A \cup B)\Big] \wedge \Big[x \notin (A \cap B)\Big]$

Verim ze to plati. Ale nedokazu to PRESNE dokazat. Dekuji.

jardofpr · 27. 01. 2019 08:38

ahoj ↑ Davisek:

skús distributívny zákon a DeMorganove pravidlá

Davisek · 27. 01. 2019 13:56

↑ jardofpr: Dekuji, poprosil bych o kontrolu. Rozepisoval jsem kroky detailne.

Budeme upravovat pravou stranu rovnice $\Big[x \in (A \cup B)\Big] \wedge \Big[x \notin (A \cap B)\Big]$ , tak aby se rovnala leve strane

$\Big[x \in (A \cup B)\Big] \wedge \Big[x \notin (A \cap B)\Big] \iff$

$\iff \Big[x \in (A \cup B)\Big] \wedge \neg\Big[x \in (A \cap B)\Big]$

$\iff \Big[\big(x \in A\big) \vee \big(x \in B\big)\Big] \wedge \neg\Big[\big(x \in A\big) \wedge \big(x \in B\big)\Big]$

$\iff \Big[\big(x \in A\big) \vee \big(x \in B\big)\Big] \wedge \Big[\big(x \notin A\big) \vee \big(x \notin B\big)\Big]$ , de Morgan

$\iff \Big[\big(x \in A\big) \wedge \big(x \notin A \vee x \notin B\big)\Big] \vee \Big[\big(x \in B\big) \wedge \big(x \notin A \vee x \notin B\big)\Big]$ , distributivni zakon

$\iff \Big[\big(x \in A \wedge x \notin A\big) \vee \big(x \in A \wedge x \notin B\big)\Big] \vee \Big[\big(x \in B \wedge x \notin A \big) \vee \big(x \in B \vee x \notin B\big)\Big]$ , distributivni zakon

$\iff \Big[FALSE \vee \big(x \in A \wedge x \notin B\big)\Big] \vee \Big[\big(x \in B \wedge x \notin A \big) \vee FALSE\Big]$

$\iff \Big[\big(x \in A \wedge x \notin B\big)\Big] \vee \Big[\big(x \in B \wedge x \notin A \big)\Big]$ , neutralita $FALSE$ vuci $\vee$

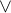
$\Big[x \in (A \cup B)\Big] \wedge \Big[x \notin (A \cap B)\Big] \iff \Big[\big(x \in A \wedge x \notin B\big)\Big] \vee \Big[\big(x \in B \wedge x \notin A \big)\Big]$

Tedy plati:

$\Big[x \in A \wedge x \notin B\Big] \vee \Big[x \notin A \wedge x \in B\Big] \iff \Big[x \in (A \cup B)\Big] \wedge \Big[x \notin (A \cap B)\Big]$

jardofpr · 27. 01. 2019 17:39

↑ Davisek:

v zásade okej ak som nič neprehliadol,

akurát ten posledný riadok kde prevrátiš obe strany implikácie je zbytočný lebo to nie je žiadna nová informácia

a v riadku 6 posledný výraz

$\dots \vee \big(x \in B \vee x \notin B\big)\Big]$

tam má byť vnútri zátvorky 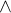$\wedge$ miesto 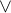$\vee$ ale ďalej píšeš FALSE tak verím že preklep

Davisek · 27. 01. 2019 18:37

↑ jardofpr:

Diky moc,jo jedna se o preklep.

Matematické Fórum

#1 27. 01. 2019 02:09

Rovnost mnozin

#2 27. 01. 2019 08:38

Re: Rovnost mnozin

#3 27. 01. 2019 13:56

Re: Rovnost mnozin

#4 27. 01. 2019 17:39

Re: Rovnost mnozin

#5 27. 01. 2019 18:37

Re: Rovnost mnozin

Zápatí