Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 02. 2016 20:41
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Function
If  is a differentiable real valued function satisfying
is a differentiable real valued function satisfying 
and  and
and 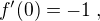 Then
Then  is
is 
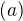 decreasing function
decreasing function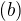 Increasing function
Increasing function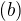 Constant function
Constant function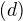 Periodic function
Periodic function
I have tried like that way  Now Multiplied both side by
Now Multiplied both side by 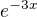
We get 
Now Integrate both side w r to  We get
We get 
So we get 
Now again integrate both side w r to  Means
Means 
So 
Now How can I Proceed after that, Thanks
Offline
#2 27. 01. 2019 16:00
Re: Function
Offline

 for
for  makes
makes 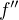 as function strictly increasing, so there is
as function strictly increasing, so there is for
for  which makes also
which makes also 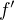 as function increasing so
as function increasing so  for
for 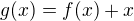 there is
there is  so
so  is increasing function
is increasing function