Matematické Fórum

adamsvek · 28. 01. 2019 11:11

Zdrávím potřeboval bych poradit s nasledujícím přikladem zda ho počítam správně.

Zadání:

Vypočítejte práci hmotného bodu o jednotkové hmotnosti, pohybující se v silovém poli 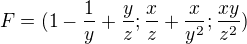$F=(1-\frac{1}{y}+\frac{y}{z};\frac{x}{z}+\frac{x}{y^{2}};\frac{xy}{z^{2}})$ z bodu A (0,1,1) do bodu B (1,1,1)

Výpočet:
$\overrightarrow{AB}=(1,0,0)$
Parametrické vyj.:
$x=t$
$y=1$
$z=1$

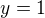
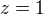
Derivace par.: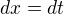
$dx=dt$
$dy=0$
$dz=0$

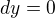
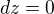
integrál
$\int_{0}^{1}1-\frac{1}{y}+\frac{y}{z}dx+0+0$
$\int_{0}^{1}1-\frac{1}{1}+\frac{1}{1}dt =(t)^{1}_{0}=1$
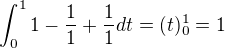
výsledek je 1 ?

prosím o radu děkuji.

Rumburak

↑ adamsvek:

Zdravím. Je otázka, zda je zadání úplné.
Práce při pohybu bodu v silovém poli obecně závisí nejen na počátečním a koncovém bodu křivky pohybu,
ale na této křivce celé (kudy je vedena). Zde křivka pohybu zadána není.
Ovšem existují speciální silová pole, v nichž dotyčná práce závisí pouze na počátečním a koncovém bodě
pohybu, tedy nikoliv na křivce samé. Taková silová pole se nazývají potenciální.

K dalšímu postupu bude vhodné budto určit křivku pohybu nebo ukázat, že dané pole "má potenciál"
a nalézt ho.

adamsvek · 28. 01. 2019 11:35

↑ Rumburak:Děkuji za reakci,ano příklad je zadaný pouze takto. Takže moje řešení by davalo smysl pokud bych jestě našel potenciál pole ?

Rumburak

↑ adamsvek:
Ano, pak by hledaná práce byla rovna rozdílu hodnot potenciálu v krajních bodech křivky.

Ale je zde i další cesta.
Platí věta, že dané hladké pole má na dané oblasti potenciál (tedy je tam potenciální) právě tehdy, má-li tam
nulovou rotaci. Pokud by toto byla vlastnost našeho pole, pak k výpočtu oné práce bychom si mohli vybrat
libovolnou (asi po částech hladkou) křivku spojující dané body v dané oblasti - takovou, aby výpočet
příslušného integrálu nebyl zbytečně komplikovaný.

MichalAld · 28. 01. 2019 12:48

Ještě připomínám, že ta rotace musí (v oblati, kudy chcme tahat křivky) existovat, všude.

Stačí aby v jednom bodě neexistovala (a všude jinde byla nulová) a už to nemusí být pravda - že hodnota integrálu nezávisí na křivce.

Rumburak

↑ MichalAld:
Zdravím a děkuji za doplnění.

adamsvek · 28. 01. 2019 13:50

↑ Rumburak:↑ MichalAld:
Děkuji zkusím si přiklad spočitat a zaměřit se na tu rotaci zda je nulová

Matematické Fórum

#1 28. 01. 2019 11:11

Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

#2 28. 01. 2019 11:32 — Editoval Rumburak (28. 01. 2019 14:41)

Re: Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

#3 28. 01. 2019 11:35

Re: Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

#4 28. 01. 2019 12:42 — Editoval Rumburak (28. 01. 2019 14:34)

Re: Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

#5 28. 01. 2019 12:48

Re: Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

#6 28. 01. 2019 12:59 — Editoval Rumburak (28. 01. 2019 14:27)

Re: Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

#7 28. 01. 2019 13:50

Re: Křivkový integrál?, výpočet pracé hmotného bodu v silovém poli

Zápatí