Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 01. 2019 17:16
Logaritmické nerovnice
Zdravím,
nemůžu přijít na řešení dvou příkladů z petákovky.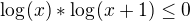
Výsledek má být 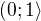
a druhý je
Zde je výsledkem 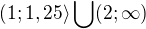
Vím jen že v druhém prípadě půjde o substituci a kvadratickou rovnici to je vše.
Offline
- (téma jako vyřešené označil(a) Proch)
#5 28. 01. 2019 17:37 — Editoval Ferdish (28. 01. 2019 17:37)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Logaritmické nerovnice
Ad druhý príklad:
Netreba substitúciu, stačí vyňať 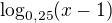 pred zátvorku a ďalej je postup analogický s prvou úlohou, čiže znova sa spýtať, kedy je súčin dvoch činiteľov nezáporný (tj. kladný alebo prinajmenšom rovný nule).
pred zátvorku a ďalej je postup analogický s prvou úlohou, čiže znova sa spýtať, kedy je súčin dvoch činiteľov nezáporný (tj. kladný alebo prinajmenšom rovný nule).
Ale odporúčam sa do toho púšťať až potom, čo vypočítaš prvý príklad, inak v tom bude chaos...
Offline
#6 28. 01. 2019 17:51
Re: Logaritmické nerovnice
Teď nevím jestli se chápeme správně, ale jestli to má být v zadání tak tam už nic jiného není.
v tomhle případě musí být jeden ze členů roven nule nebo zápornému číslu, aby to mohlo platit, ale zase je to jen moje dedukce.
Offline
#9 28. 01. 2019 18:21
Re: Logaritmické nerovnice
↑ Proch: Nepoznam matematicke a nematematicke riesenie ulohy, ale iba spravne a nespravne. A ak vyuzijes skutocnosti o znamienku sucinu dvoch cisel spolu s vlastnostami logaritmickej funkcie, ide podla mna o spravne riesenie.
Offline
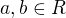 je
je 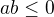 ?
?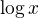 a
a 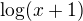 a uvazuj o ich sucine, teda iba o znamienku toho sucinu.
a uvazuj o ich sucine, teda iba o znamienku toho sucinu.