Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Binomial coefficients (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 01. 2019 06:48
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Binomial coefficients
Evaluation of 
Offline
- (téma jako vyřešené označil(a) byk7)
#2 28. 01. 2019 23:15 — Editoval laszky (29. 01. 2019 02:25)
Re: Binomial coefficients
Offline
#3 29. 01. 2019 18:48 — Editoval stuart clark (29. 01. 2019 18:51)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Binomial coefficients
Thanks ↑ laszky:.
I have one more binomial problem
Evaluation of  For
For 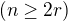
please see that problem
Offline
#4 30. 04. 2019 16:43
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Binomial coefficients
@ Laszky I am Trying that problem using
Coefficient of 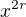 in
in ![kopírovat do textarea $(1+x+x^2)^{n}=\bigg[1+x(1+x)\bigg]^n=\bigg[\bigg(x+\frac{1}{2}\bigg)^2+\frac{3}{4}\bigg]^n$](/mathtex/7e/7e40d627371f255463bad5e4c7d80f43.gif)
But could not find end result, please show me how to get it
Thank You
Offline
#5 02. 05. 2019 16:24 — Editoval Marian (02. 05. 2019 16:25)
Re: Binomial coefficients
↑ stuart clark:
Note to your first problem:
There is a free paper from Butler (2010), see the PDF version here, that discuss your sum. Also, certain generalizations are mentioned that could be of some importance to you.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Binomial coefficients (TOTO TÉMA JE VYŘEŠENÉ)
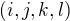 ,
,  , is
, is 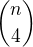 ,
,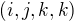 ,
,  , is
, is 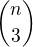 ,
,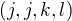 ,
,  , is
, is 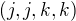 ,
,  , is
, is  .
.![kopírovat do textarea $S(n)=\displaystyle \mathop{\sum\sum\sum\sum}_{1\leq i \leq j<k\leq w \leq n}1 = \left[\binom{n}{4}+\binom{n}{3}\right] + \left[\binom{n}{3}+\binom{n}{2}\right] = \binom{n+1}{4}+\binom{n+1}{3} = \binom{n+2}{4}$](/mathtex/e1/e15fbb6887c9484c3b11ed977da42d83.gif)
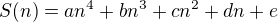 has to be polynomial of degree
has to be polynomial of degree  (4 sums) and compute
(4 sums) and compute 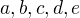 by solving the system of five equations
by solving the system of five equations 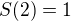 ,
, 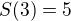 ,
, 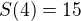 ,
, 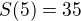 and
and 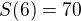 .
.