Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 29. 01. 2019 15:48 — Editoval Al1 (29. 01. 2019 15:49)
Re: Průběh funkce
↑ zzzz1:
Zdravím,
jen upozorním na tvou chybu při derivování.
Upravila jsi předpis do tvaru 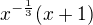 , derivuješ součin. První sčítanec v tvém výsledku je správný, druhý ne. Derivace ( x+1) je 1 (to je dobře), ale
, derivuješ součin. První sčítanec v tvém výsledku je správný, druhý ne. Derivace ( x+1) je 1 (to je dobře), ale 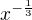 se nederivuje a ani jinak nemění.Ty jsi napsala
se nederivuje a ani jinak nemění.Ty jsi napsala 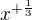
Offline

![kopírovat do textarea $f(x)=\frac{|1+x|}{\sqrt[3]{x}}$](/mathtex/d8/d8a419eaa838089aa4f777d8a6ecf6a6.gif) . Mám vypočítané
. Mám vypočítané  .
.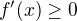 tak mi vyjde nerovnost
tak mi vyjde nerovnost ![kopírovat do textarea $1+x\leq 3\sqrt[3]{x^5}$](/mathtex/d4/d49c7d0cdd4637726d54e55efaa4ed3d.gif) a dál nevím co s tím.
a dál nevím co s tím.![kopírovat do textarea $\left(\frac{1+x}{\sqrt[3]{x}}\right)'=\left(x^{-\frac{1}{3}}+x^{\frac{2}{3}}\right)'=-\frac{1}{3}x^{-\frac{4}{3}}+\frac{2}{3}x^{-\frac{1}{3}}=\frac{2x-1}{3x\sqrt[3]{x}}$](/mathtex/60/60bc51c69798474488293807ff02b07c.gif)
