Matematické Fórum

jardasmid · 27. 05. 2009 19:11

Mohl by mi někdo poradit, jak zjistit, jestli řada konverguje absolutně/neabsolutně nebo diverguje? Vůbec to nechápu.

$\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{\sqrt{k}}$

Johny · 27. 05. 2009 19:25

jardasmid napsal(a):
Mohl by mi někdo poradit, jak zjistit, jestli řada konverguje absolutně/neabsolutně nebo diverguje? Vůbec to nechápu.

$\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{\sqrt{k}}$

Pro ověření neabsolutní konvergence použij Leibnitzovo kriterium. To je jednoduche, to jsou 3 kriteria. A pro důkaz absolutní konvergence třeba srovnávací :).

misickacz · 27. 05. 2009 19:29

↑ Johny:
tu absolutní konvergenci určíš z absolutní hodnoty toho výrazu, takže ti zmizí ta (-1) v čitateli

jardasmid · 27. 05. 2009 20:56

Takže jestli jsem dobře pochopil, to co je na wikipedii, tak to napíšu jako
$\sum_{k=1}^{\infty} (-1)^{k-1}\frac{1}{\sqrt{k}}$
kde
$\frac{1}{\sqrt{k}} = a_k$
pak ověřím limitu
${\lim}\limits_{k \to \infty}a_k=0$
pak jestli je vždy $a_k > 0$ a jestli je řada $\sum_{k=1}^{\infty}a_k$ klesající, potom bude řada konvergentní? A když pak budu dělat limitu k absolutní hodnotě a_k, tak musí být reálné číslo ... pochopil jsem to dobře, nebo kecám blbosti?

Johny · 27. 05. 2009 21:10 — Editoval Johny (27. 05. 2009 21:11)

jardasmid napsal(a):
Takže jestli jsem dobře pochopil, to co je na wikipedii, tak to napíšu jako
$\sum_{k=1}^{\infty} (-1)^{k-1}\frac{1}{\sqrt{k}}$
kde
$\frac{1}{\sqrt{k}} = a_k$
pak ověřím limitu
${\lim}\limits_{k \to \infty}a_k=0$
pak jestli je vždy $a_k > 0$ a jestli je řada $\sum_{k=1}^{\infty}a_k$ klesající, potom bude řada konvergentní? A když pak budu dělat limitu k absolutní hodnotě a_k, tak musí být reálné číslo ... pochopil jsem to dobře, nebo kecám blbosti?

Jak jsem psal víše , musíš použít nějaké kritérium pokud víš co myslím. To co jsi napsal moc nechápu. Tu limitu(enteho členu) co tam píšeš ti akorát řekne, zda to nebude konvergovat. Pokud je limita ruzná od nuly tak řada nekonverguje.

Marian · 27. 05. 2009 21:57 — Editoval Marian (27. 05. 2009 21:57)

↑ Johny:↑ misickacz:

Matematicky jsou vaše tvrzení velmi nepřesná.

Především však alternující řada je taková, která se dá zapsat ve tvaru $\sum_{k=1}^{\infty}(-1)^{k-1}a_k$ , kde $a_k>0$ pro všechna přirozená čísla "k". V našem případě bude $a_k:=\frac{1}{\sqrt{k}}$ pro všechna přirozená čísla "k". Chceme-li použít Leibnizovo kriterium, musí být splněno několik dílčích podmínek:
(1) ověří se, že platí $\lim_{k\to\infty}a_k=0$ - splněno;
(2) ověří se, že posloupnost {a_k} je klesající - splněno.

Tedy Leibnizovo kriterium dává konvergenci této řady, tj. tato řada se dá sečíst a její součet lze reprezentovat některým reálným číslem na číselné ose.

Johny · 27. 05. 2009 22:03 — Editoval Johny (27. 05. 2009 22:10)

↑ Marian:

Já jsem myslel nutnou podmínku konvergence. Tedy pokud řada konverguje tak jeji limita je nula. Nerozebíral jsem žádné kriterium, které děláte.

Marian · 27. 05. 2009 22:19

↑ Johny:
Leibnizovo kriterium dává hned relativní konvergenci, nutná podmínka tedy není třeba (zdá se) - jenže ona sama je obsažena v Leibnizově kriteriu. Tedy toto kriterium zvládá několik věcí naráz.

Nechápu ale především gramatickou strukturu vět

Pro ověření neabsolutní konvergence použij Leibnitzovo kriterium. To je jednoduche, to jsou 3 kriteria. A pro důkaz absolutní konvergence třeba srovnávací :).

Především logická koherence prvních dvou vět mi uniká - dostávám se do sporu.

Souhlasím se srovnávacím kriteriem pro absolutní konvergenci, nicméně přímější mi připadá použití integrálního kriteria, jehož podmínky jsou splněny a výpočet je dle mého názoru rychlý.

Johny · 27. 05. 2009 22:32 — Editoval Johny (27. 05. 2009 22:33)

↑ Marian:

Omlouvám se, já nejsem takový pedant jako Vy :). Volil jsem špatná slova.Patrně budete nějaký pedagog s baňské :). Nevím proč jsou ve sporu první dvě věty. Učil jsem se že se u leibnitzova kriteria dělají 3 podmínky pro splnění :
1- entý člen větší,roven nule;
2 - (n+1) člen je menší roven en-tému členu;
3 - limita řady je nula;

Jasně proč ne integrální kritérium, ale já třeba nerad integruji :D

Marian · 27. 05. 2009 22:43 — Editoval Marian (27. 05. 2009 22:44)

↑ Johny:
Budu přesnější - Leibnizovo kriterium je jediné kriterium, nejsou to tedy tři kriteria (viz tvá věta druhá - dovolím si tykání) - odtud spor 1=3. Souhlasím s náhradou za slovo "podmínky".

Hodnocená typu "pedant" patří k těm lichotivým, slyšel jsem i horší (ale i ta mě potěší). Pedagog jsem a s báňskou mám taky co do činění (jen ta předložka "s" tam nesedí v příspěvku výše, nahradil bych předložkou "z").

Lebnizovo kriterium se týká alternujících řad, tedy řad, které jsem popsal výše. Není tedy třeba již tvé podmínky první, která kopíruje částečně definici alternující řady.

A z historického hlediska (a jako matematik germanista) připomínám častou chybu nejen studentů, že se nepíše Leibnitzovo kriterium, ale Leibnizovo kriterium.
:-)

jardasmid · 27. 05. 2009 23:07

Díky za rady, ale jelikož jsem natvrdlej, jak zjistím, jestli je absolutně konvergující. To musím udělat $\lim_{k\to\infty}|a_k|=0$ ?

Marian · 27. 05. 2009 23:10

↑ jardasmid:
Musíš zjistit, jak to vypadá s konvergencí řady, kterou vytvoříš z řady původní tak, že umístíš všechny sčítance do absolutních hodnot, tj. vytvoříš řadu
$\sum_{n=1}^{\infty}\left |(-1)^{k-1}\cdot\frac{1}{\sqrt{k}}\right |=\sum_{k=1}^{n}\frac{1}{\sqrt{k}}.$
Jak bylo napsáno, stačí použít třeba integrální nebo srovnávací kriterium.

jardasmid · 28. 05. 2009 17:38

K tomu integrálnímu kritériu (jiný příklad) ...
Když mám $\sum_{k=1}^{\infty}\frac{1}{2k+3}$
tak ten integrál vypadá takto:
$\int_{1}^{\infty}\frac{1}{2x+3}dx = \mathop{\lim}\limits_{a \to \infty}[\frac{\ln(2k+3)}{2}]^{a}_1 = \infty$ a když je to nekonečno, tak to diverguje a konvergovalo by to když to bude rovno nějakému R? Snad už poslední blbý dotaz :-)

lukaszh

↑ jardasmid:
R je množina reálnych čísel. Ak je to rovné nejakému 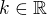$k\in\mathbb{R}$ , potom rad konverguje.

jardasmid · 28. 05. 2009 18:18

Super. Budete se zlobit, když ještě budu otravovat? Jak na řadu
$\sum_{k=1}^{\infty} \frac{1}{k^2+1}$
To také udělám integrálním kritériem? Mi tam pak ale vznikne ${\lim}\limits_{a \to \infty}[\frac{\ln(x^2+1)}{2x}]^a_1$ a pak tam bude $\frac{\ln(\infty^2+1)}{2\infty}-\frac{\ln2}{2}$ a tu limitu asi neudělám ...

Kondr · 28. 05. 2009 19:08

↑ jardasmid:Chybu máš ve výpočtu integrálu $\int_0^{\infty} \frac{1}{x^2+1}=\lim_{a\to\infty} [\arctan x]_0^{a}=\frac{\pi}{2}$ . Zde ale stačilo použít srovnávací kritérium, víme totiž, že řada $\sum \frac{1}{k^2}$ konverguje.

Jinak pokud vyjde limita $\infty/\infty$ , tak je dobré buď použít l'Hospitala, nebo alespoň odhad: (logaritmus polynomu)/polynom jde do nuly, exponenciála/polynom do nekonečna apod.

jardasmid · 28. 05. 2009 19:28

Díky moc. A dneska už opravdu poslední dotaz. Jak podle definice spočítat součet řady:
$\sum_{k=1}^{\infty}\frac{1}{(4k-3)(4k+1)}$

Pavel Brožek · 28. 05. 2009 19:46

↑ jardasmid:

$\sum_{k=1}^{\infty}\frac{1}{(4k-3)(4k+1)}=\lim_{n\to\infty}\sum_{k=1}^n\frac{1}{(4k-3)(4k+1)}=\lim_{n\to\infty}\sum_{k=1}^n$\frac{\frac14}{4k-3}-\frac{\frac14}{4k+1}$=\nl \lim_{n\to\infty}$\frac14\sum_{k=1}^n\frac{1}{4k-3}-\frac14\sum_{k=1}^n\frac{1}{4k+1}$=\lim_{n\to\infty}$\frac14\sum_{k=1}^n\frac{1}{4k-3}-\frac14\sum_{k=2}^{n+1}\frac{1}{4k-3}$=\nl \lim_{n\to\infty}$\frac14\cdot\frac{1}{4\cdot1-3}-\frac14\cdot\frac{1}{4\cdot(n+1)-3}$=\ldots$

jardasmid · 28. 05. 2009 22:08

↑ BrozekP:
Děkuju

Matematické Fórum

#1 27. 05. 2009 19:11

Číselné řady

#2 27. 05. 2009 19:25

Re: Číselné řady

jardasmid napsal(a):

#3 27. 05. 2009 19:29

Re: Číselné řady

#4 27. 05. 2009 20:56

Re: Číselné řady

#5 27. 05. 2009 21:10 — Editoval Johny (27. 05. 2009 21:11)

Re: Číselné řady

jardasmid napsal(a):

#6 27. 05. 2009 21:57 — Editoval Marian (27. 05. 2009 21:57)

Re: Číselné řady

#7 27. 05. 2009 22:03 — Editoval Johny (27. 05. 2009 22:10)

Re: Číselné řady

#8 27. 05. 2009 22:19

Re: Číselné řady

#9 27. 05. 2009 22:32 — Editoval Johny (27. 05. 2009 22:33)

Re: Číselné řady

#10 27. 05. 2009 22:43 — Editoval Marian (27. 05. 2009 22:44)

Re: Číselné řady

#11 27. 05. 2009 23:07

Re: Číselné řady

#12 27. 05. 2009 23:10

Re: Číselné řady

#13 28. 05. 2009 17:38

Re: Číselné řady

#14 28. 05. 2009 18:06 — Editoval lukaszh (28. 05. 2009 18:07)

Re: Číselné řady

#15 28. 05. 2009 18:18

Re: Číselné řady

#16 28. 05. 2009 19:08

Re: Číselné řady

#17 28. 05. 2009 19:28

Re: Číselné řady

#18 28. 05. 2009 19:46

Re: Číselné řady

#19 28. 05. 2009 22:08

Re: Číselné řady

Zápatí