Matematické Fórum

Roscelinius · 31. 01. 2019 18:25

Dobrý den,
V Matematice pro porozumění a praxi III/2 od Musilvých je příklad 13.14 na Cauchy Riemannovy podmínky trochu jinak, nejedná se přímo o jejich vyjádření v polárních souřadnicích jak je běžné.
Mějme 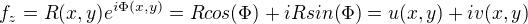$f_{z}=R(x,y)e^{i\Phi (x,y)}=Rcos(\Phi )+ iRsin(\Phi )=u(x,y)+iv(x,y)$
z toho se vypočítají parciální derivace u a v podle x a y a ty se porovnají podle Cauchyho Riemannových podmínek a upravý, čímž má nakonec vyjít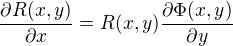
$\frac{\partial R(x,y)}{\partial x }=R(x,y)\frac{\partial \Phi (x,y)}{\partial y }$
$\frac{\partial R(x,y)}{\partial y }=-R(x,y)\frac{\partial \Phi (x,y)}{\partial x }$
Pomohli byste mi prosím s postupem (stačí slovně)? Vvůbec nevím jak by mohly goniometrické funkce vypadnou, napadá mě jen, že by se dosadilo 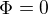$\Phi =0$ , což by vysvětlovalo vymizení částí u kterých je sinus, ale nevím proč by se to tak udělalo.
díky moc

jardofpr · 01. 02. 2019 00:56

ahoj ↑ Roscelinius:

mne to pripadá že je to nejak takto (označenie používam 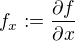$f_x:=\frac{\partial f}{\partial x}$ )

systém pre CR podmienky pre danú funkciu je 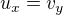$u_x=v_y$ , $u_y = -v_x$

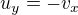
t.j.

$R_x\cos{\Phi}-R\Phi_x\sin{\Phi}=R_y\sin{\Phi}+R\Phi_y\cos{\Phi}$
$R_y\cos{\Phi}-R\Phi_y\sin{\Phi}=-R_x\sin{\Phi}-R\Phi_x\cos{\Phi}$

pre ľubovoľné 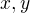$x,y$ teda má platiť že

$\begin{bmatrix}\cos{\Phi}&-\sin{\Phi}\\ \sin{\Phi}&\cos{\Phi}\end{bmatrix}\begin{bmatrix}R_x-R\Phi_y\\ R_y+R\Phi_x\end{bmatrix}=\begin{bmatrix}0\\ 0\end{bmatrix}$

matica v rovnici je regulárna s determinantom 1 pre ľubovoľné 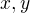$x,y$ , t.j. nulový musí byť na ľavej strane vektor,
z toho sú podľa mňa rovnice ktoré uvádzaš

Roscelinius

↑ jardofpr:
Moc děkuji. Jen pro ujasnění - moc jsem nepochopil o jakém vektoru v poslední větě mluvíš - je li první matice regulární s determinantem 1, znamená to jednoduše, že nemůže být nulová a musí být tedy nulová druhá matice?

jardofpr · 01. 02. 2019 10:09

↑ Roscelinius:

Roscelinius napsal(a):
↑ jardofpr:
Moc děkuji. Jen pro ujasnění - moc jsem nepochopil o jakém vektoru v poslední větě mluvíš

tá matica vpravo v maticovom zápise toho systému dvoch rovníc je myslená ako typ 2x1, teda vektor ktorého

prvá zložka je 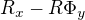$R_x-R\Phi_y$ a druhá zložka je $R_y+R\Phi_x$

Roscelinius napsal(a):
↑ jardofpr:
je li první matice regulární s determinantem 1, znamená to jednoduše, že nemůže být nulová a musí být tedy nulová druhá matice?

myšlienka za tým je že keď si zvolíš ľubovoľne ale pevne konkrétne 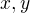$x,y$ , tá matica predstavuje regulárnu
lineárnu transformáciu v 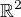$\mathbb{R}^2$ (pre pevnú voľbu má číselné koeficienty)

ale regularita znamená že jediný vektor z 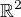$\mathbb{R}^2$ ktorý sa zobrazí na nulový vektor je nulový vektor,
t.j. pre zložky 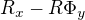$R_x-R\Phi_y$ a $R_y+R\Phi_x$ (pri pevnej voľbe x,y sú to tiež čísla) platí že sa rovnajú nule

keďže je to nezávislé na voľbe 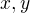$x,y$ , platí to pre všetky voľby $x,y$ ,

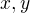t.j. 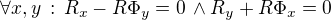$\forall x,y \,:\, R_x-R\Phi_y = 0\,\wedge R_y+R\Phi_x=0$ čo už sú tvoje rovnice

Matematické Fórum

#1 31. 01. 2019 18:25

Cauchy Riemannovy podmínky - Musilová

#2 01. 02. 2019 00:56

Re: Cauchy Riemannovy podmínky - Musilová

#3 01. 02. 2019 07:10 — Editoval Roscelinius (01. 02. 2019 07:11)

Re: Cauchy Riemannovy podmínky - Musilová

#4 01. 02. 2019 10:09

Re: Cauchy Riemannovy podmínky - Musilová

Roscelinius napsal(a):

Roscelinius napsal(a):

Zápatí