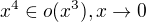Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » O využití McLaurinovy řady pro výpočet limity
#1 01. 02. 2019 19:48
O využití McLaurinovy řady pro výpočet limity
Mám limitu 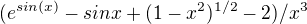 , když x jde do nuly, rozvinu jí pomocí McLaurinovy řady, ale v závěru mi vychází.
, když x jde do nuly, rozvinu jí pomocí McLaurinovy řady, ale v závěru mi vychází.
Podle výsledků by měla limita vycházet 1/6 a x^4 by se tedy měly odečíst.
Nevím jestli není třeba problém v rozvoji (1 - x^2)^(1/2), který jsem dělal takto (1 + (-x^2))^(1/2).
Offline
#3 01. 02. 2019 20:30
Re: O využití McLaurinovy řady pro výpočet limity
↑ Jj: Prominte, nepřesně jsem se vyjádřil.
Ten jsem použil, resp. mi vyšel také a u rozvoje e^(sinx) mám též -x^4/8, což mi dohromady dává opět -x^4/4 a po odečtení všech rozvojů mám (x^3/6 - x^4/4 + o(x^4))/x^3
Offline
#5 01. 02. 2019 20:52
Re: O využití McLaurinovy řady pro výpočet limity
↑ Stýv: Je mi to divné, protože u většiny příkladů se taková mocnina odečte, mám pocit.
Vzhledem k tomu, že x^4 je menší než x^3, tak je v pohodě to x^4 schovat do o(x^3) vzhledem k tomu, že je oproti x^3 zanedbatelné?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » O využití McLaurinovy řady pro výpočet limity