Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 02. 2019 00:00 — Editoval laszky (13. 02. 2019 02:41)
Re: Irrational Integration
Offline
#3 13. 02. 2019 14:18 — Editoval krakonoš (13. 02. 2019 14:27) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš. Důvod: uz vyreseno
#4 14. 02. 2019 11:32
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Irrational Integration
Thanks ↑ laszky:.
please have a look on that problem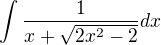
Offline
#5 15. 02. 2019 03:37
Re: Irrational Integration
Offline
#6 17. 02. 2019 14:07
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Irrational Integration
Thanka ↑ laszky:.
please have a look 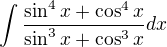
Offline
#7 25. 02. 2019 16:21
#8 26. 02. 2019 13:27 — Editoval stuart clark (26. 02. 2019 13:33)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Irrational Integration
Thanks ↑ jardofpr:
I have solved like this way
Let 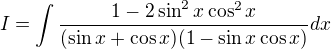

Now put  and
and  and
and 

and using partial fraction
Offline

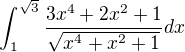
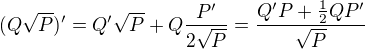 and
and 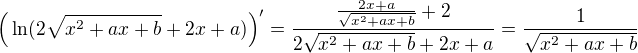
 ,
,  ,
,  and
and  such that
such that 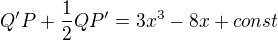 we find out that
we find out that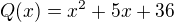 and
and 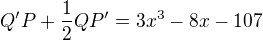 .
.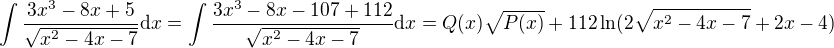
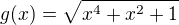 , there holds
, there holds
![kopírovat do textarea $\int^{\sqrt{3}}_{1}\frac{3x^4+2x^2+1}{\sqrt{x^4+x^2+1}}\,\mathrm{d}x = \Bigr[x\sqrt{x^4+x^2+1}\Bigr]_1^{\sqrt{3}} = \sqrt{3}(\sqrt{13}-1)$](/mathtex/ca/caf398cb11cc801b974ac55e14b24e48.gif)
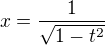 we get
we get and
and  .
.
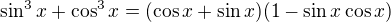
 such that
such that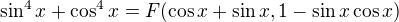
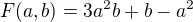
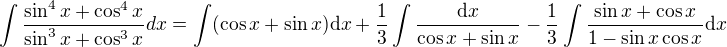

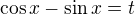 as
as ![kopírovat do textarea $1-\sin{x}\cos{x} = \frac{1}{2}[1+(\cos{x}-\sin{x})^2]$](/mathtex/3a/3adeb4eed78d8cc7c17a6a53dc3db363.gif)