Matematické Fórum

Roscelinius

Dobrý den,
zamotal jsem se do Laplaceovy transformace a potřeboval bych poradit.
Pro výpočet jednoduchého obrazu F(z) konstantní funkce f(t)=K platí: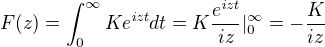
$F(z)= \int_{0}^{\infty }K e^{\textit{izt}}dt= K \frac{e^{\textit{izt}}}{iz}|_{0}^{\infty }=-\frac{K}{iz}$
vysvětlili byste mi prosím jak se vypočítal onen nevlastní integrál? Pokud použijeme Newtonův-Leibnittzův vzorec, odpovídá konečný výsledek hodnotě integrálu v nule, nevím ale jak se došlo k závěru, že hodnota integrálu v nekonečnu je nulová. Je to přeci limita: $\lim_{t\to\infty }K \frac{e^{\textit{izt}}}{iz}$ , nebo ne?

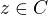S odstupem mě napadlo jestli nulovost integrálu v nekonečnu není už způsobena definicí Laplaceovy transformace ve které se f(t) předpokládá taková, že Riemanův integrál $Lf(z)= F(z)=\int_{0}^{\infty }f(t) e^{izt}dt$ je absolutně konvergentní alespoň v jednom $z\in C$ . Běžně se ale Laplaceova transformace definuje takto: 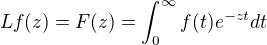$Lf(z)= F(z)=\int_{0}^{\infty }f(t) e^{-zt}dt$ . Jak mám rozumět definici pomocí $e^{izt}$ ? Jako $e^{izt}=e^{i(x+iy)t}=e^{ixt-yt}=e^{ixt}e^{-yt}$ , ve které pro $t-> \infty$ část $e^{ixt}$ "osciluje" na jednotkové kružnici a o konvergenci k nule se stará část $e^{-yt}$ ?

Děkuji
(omlouvám se za překlep v názvu přízpěvku)

Brano · 14. 02. 2019 15:29

Aj ja som videl skor tu druhu definiciu, ale principialne je to jedno.

ano konvergenciu zabezpeci clen $e^{-yt}$ len musis predpokladat $y>0$ t.j. transformacia bude definovana iba pre takez $z$ ktore splnaju $Im(z)>0$

Matematické Fórum

#1 11. 02. 2019 22:56 — Editoval Roscelinius (12. 02. 2019 07:16)

Výločet integrálu v Laplaceovy transformaci

#2 14. 02. 2019 15:29

Re: Výločet integrálu v Laplaceovy transformaci

Zápatí