Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 02. 2019 09:20
Ohmův zákon - napětí
Ahoj, Prosim Vas. Ucim se elektrinu a magnetismus a jsem u ohmova zakona konkretne u napeti. Jsem u prikladu kde je jeden zdroj napeti a spotrebic. Chapu to, ze kdyz ma zdroj elektromotoricke napeti 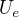 , tak pri mereni voltmetrem je stejne jako svorkove nezatizeneho zdroje
, tak pri mereni voltmetrem je stejne jako svorkove nezatizeneho zdroje 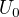 . Ale nerozumim proc se snizi napeti pri pripojedeni zateze napr odporu. Aby jste mi rozumeli podle vypoctu ano, ale do tehle chvile byli vsechny jevy vysvetleny na atomarni urovni. K tomuto deji byla jedna veta Pripojeni spotrebice, cili zatizeni zdroje zpusobuje ubytek naboju na jeho polech. Rozdil potencialu mezi svorkami zdroje se zmensuje, a mensi se i svorkove napeti.
. Ale nerozumim proc se snizi napeti pri pripojedeni zateze napr odporu. Aby jste mi rozumeli podle vypoctu ano, ale do tehle chvile byli vsechny jevy vysvetleny na atomarni urovni. K tomuto deji byla jedna veta Pripojeni spotrebice, cili zatizeni zdroje zpusobuje ubytek naboju na jeho polech. Rozdil potencialu mezi svorkami zdroje se zmensuje, a mensi se i svorkove napeti.
Ja rozumim tomu, ze kdyz se snizi naboj na polech zdroje, tak se snizi i velikost potencialu. Ale cemu nerozumim je, proc se ten naboj snizi. Vsak kdyz zkratuji obvod, tak se snizuje naboj mnohem rychleji nez s odporem a svorkove napeti je pritom stale stejne velke 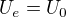 . Kam tedy prijde cast naboje pri pripojeni spotrebice, ze se snizi napeti vice nez pri zkratovani ?
. Kam tedy prijde cast naboje pri pripojeni spotrebice, ze se snizi napeti vice nez pri zkratovani ?
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
- (téma jako nevyřešené označil(a) Meglun)
#2 23. 02. 2019 12:25 — Editoval edison (23. 02. 2019 12:27)
Re: Ohmův zákon - napětí
Řekl bych, že si to moc komplikuješ a tak ses do toho zamotal. Na svorkách zatíženého zdroje je: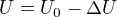
A to  je u zdroje triviální konstrukce dáno jeho vnitřním odporem, tedy
je u zdroje triviální konstrukce dáno jeho vnitřním odporem, tedy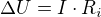
No a pak máme ty svorky. Mají nějakou kapacitu a ta je nabitá na náboj: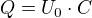
A protože napětí kleslo, náboj se snížil o 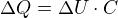
Offline
#3 23. 02. 2019 12:35
Re: Ohmův zákon - napětí
Ještě k té atomární úrovni:
Tu na téhle úrovni zobecnění nejde praktikovat. Na atomární úrovni je odpor vodiče v transformátoru něco poněkud jiného, než např. odpor galvanického článku.
A pak návrat do reality: 99% zdrojů je elektronických a tam nemá smysl to na atomární úrovni řešit. Je to věc vlastností daného stabilizačního obvodu a jeho základem může být třeba integrovaný obvod obsahující 100 tranzistorů. Navíc pak takový zdroj většinou nevykazuje čistě odporové chování.
Offline
#4 23. 02. 2019 12:54
Re: Ohmův zákon - napětí
A ještě poznámka k tomu zkratu:
Při něm je U = 0, případně U = I.R, pokud předpokládáme, že jsme zkrat realizovali reálným vodičem s nenulovým odporem.
Taky zase poznámka k praxi: Elektronický zdroj se při zkratu na chvíli vypne, nebo sníží proud na nějakou minimální hodnotu a čeká na odzkratování, případně drží nějaký pevně daný maximální proud. (A ještě 100 dalších, poněkud minoritních možností)
Offline
#5 23. 02. 2019 13:38 — Editoval MichalAld (23. 02. 2019 13:49)
Re: Ohmův zákon - napětí
Meglun napsal(a):
Chapu to, ze kdyz ma zdroj elektromotoricke napeti
, tak pri mereni voltmetrem je stejne jako svorkove nezatizeneho zdroje
.
Pokud si myslíš že chápeš cokoliv, co obsahuje pojem "elektromotorické napětí", tak se nejspíš hluboce mýlíš. A pokud tomu nevěříš, můžeš kouknout tady a případně ještě i tady .
Osobně bych doporučoval představu "elektromotorického napětí" používat velmi opatrně, nebo ještě lépe vůbec - a vystačit si s představou napětí naprázdno - tj. že reálný zdroj se skládá z "ideálního zdroje" a sériového odporu.
Offline
#6 23. 02. 2019 13:46
Re: Ohmův zákon - napětí
Pokud jde o vnitřní odpor zdroje - on "zdroj" je dost široký pojem. Může to zahrnovat celou řadu "krabiček" a každá z nich má vnitřní mechanismus jiný.
Pokud za "zdroj" budeme považovat třeba zásuvku co máš v bytě, nebo třeba transformátor, co je do ní zapojený - no tak když půjdeš po těch vodičích dál, tak narazíš cestou na několik dalších transformátorů a nakonec dojdeš (s velkou pravděpodobností) k synchronnímu generátoru.
Tenhle generátor se točí konstantní rychlostí (ono to v síti, kde běží tyhle generátory paralelně ani moc jinak nejde) - a napětí odpovídá těm otáčkám. Takže celý vnitřní odpor takovéhoto "zdroje" je opravdu tvořen téměř jen odporem těch dráhů, co jsou jimi navinutá vinutí generátorů a transformátorů a drátů, které to rozvádějí - z elektrárny až k tobě domů.
Chemické zdroje naproti tomu mají svůj vnitřní odpor pocházející převážně z toho, že se ty nabité částice v elektrolytu nedokáží pohybovat moc rychle. Ale mmch - když už se pídíš po "atomárním principu" vnitřního odporu elektrochemických zdrojů - zamyslel ses někdy vůbec nad tím, proč mají odpor ("z atomárního principu") i obyčejné kovové vodiče ?
Offline
#7 23. 02. 2019 15:41
Re: Ohmův zákon - napětí
↑ MichalAld:
to ze maji odpor vodice a obecne odpor jsem se snazil take zkoumat. Myslim, ze tim jak rotuji elektrony blize jadru nez valencni, maji vetsi rychlost a zaroven na ne pusoby vetsi el. sila (dostrediva) a proto je treba je zahrat aby se rozpohybovali rychleji a mohli se "utrhnout"
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#8 23. 02. 2019 15:46 — Editoval Meglun (23. 02. 2019 15:46)
Re: Ohmův zákon - napětí
Obecne nevim jestli se tim mam takto do hloubky zabyvat, kdyz me to zajima. Nebo jestli nemam projet to co je ve stredoskolske ucebnici a pocitat s tim, ze vysokoskolske publikace se temito otazkami zabyvaji
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#9 23. 02. 2019 17:51
Re: Ohmův zákon - napětí
Meglun napsal(a):
Obecne nevim jestli se tim mam takto do hloubky zabyvat, kdyz me to zajima. Nebo jestli nemam projet to co je ve stredoskolske ucebnici a pocitat s tim, ze vysokoskolske publikace se temito otazkami zabyvaji
Pokud tě to zajímá, tak je určitě dobré po věcech pátrat - ale musíš být připravený na to, že né všechno má jednoduché vysvětlení. Ani ve VŠ učebnicích zdaleka nemusíš najít všechno.
Například vše, co se týká vlastností pevných látek (jako třeba proč vůbec vedou el. proud, nebo proč vůbec drží pohromadě) lze alespoň trochu správně pochopit jen s použitím kvantové mechaniky - a to je dost pokročilá část fyziky, o které většina lidí ani neví, že vůbec existuje....
Offline
#10 25. 02. 2019 19:29
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Ohmův zákon - napětí
↑ Meglun:
Ohmův zákon se dá odvodit i v klasickém elektromagnetismu:

Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#11 26. 02. 2019 08:31
Re: Ohmův zákon - napětí
KennyMcCormick napsal(a):
↑ Meglun:
Ohmův zákon se dá odvodit i v klasickém elektromagnetismu:
Až na ten "pásový model" a důvod, proč se elektrony s něčím srážejí (a proč se sráží tak málo, a né s každým atomem, co cestou potkají).
Offline
#12 26. 02. 2019 22:30
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Ohmův zákon - napětí
Až na ten "pásový model"
Ano, to je pravda. 🙂
(a proč se sráží tak málo, a né s každým atomem, co cestou potkají)
Aha... Je to proto, že elektron může protunelovat skrz atom?
(Jestli se nepletu, tak tohle nepotřebujeme v tom odvození vědět, protože nám stačí, že střední volná dráha  je konstanta a nemusíme vědět, jestli je tak velká, jak předpovídá klasická fyzika, nebo jiná.)
je konstanta a nemusíme vědět, jestli je tak velká, jak předpovídá klasická fyzika, nebo jiná.)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#13 26. 02. 2019 23:45
Re: Ohmův zákon - napětí
KennyMcCormick napsal(a):
Aha... Je to proto, že elektron může protunelovat skrz atom?
To já nevím, nikdy jsem neviděl žádný matematický model kovové látky - myslím jako hrst atomových jader spolu se stejnou hrstí elektronů ... i když možná že dnes už by něco takového šlo spočítat, kdo ví.
Tunelováním se to myslím nazývá pokud je energie částice nižší než energie bariéry, pokud je vyšší, tak se to asi nenazývá nijak...
Podle mě je spíš trik v tom Pauliho principu - prostor mezi atomovými jádry je "vyplněn" (z hlediska Pauliho prinicipu) elektrony s nízkou energií, takže už se tam žádný další nevejde a jádra se nemohou dostat blíže k sobě .... ale pro elektrony s vyšší energií je tam místa kupa.
Z jiného pohledu o tom zase píše Feynman ve 3. díle přednášek - ale tam používá k popisu jen diferenční rovnice - že má elektron jistou amplitudu přeskoku k předchozímu a následujícímu atomu - a krásně to vyjde, že řešením je postupná vlna - buď dopředu nebo zpět - což odpovídá pohybu částice konstantní rychlostí.
KennyMcCormick napsal(a):
(Jestli se nepletu, tak tohle nepotřebujeme v tom odvození vědět, protože nám stačí, že střední volná dráha
je konstanta a nemusíme vědět, jestli je tak velká, jak předpovídá klasická fyzika, nebo jiná.)
No jo, v "tomhle" odvození to nepotřebujeme, ale musíme použít pár dodatečných předpokladů, které musíme "vytáhnout z rukávu". Takže to není úplně odvození "v klasickém elektromagnetismu" - ale "v klasickém elektromagnetismu s hrstí dodatečných předpokladů" - a platnost těch předpokladů bychom měli ověřit ještě i na nějakých jiných jevech.
Ale pokud já vím, tak skoro všechny vlastnosti látek (zejména pevných) se odvozují zkombinováním klasické fyziky, kvantové mechaniky a statistické mechaniky (ta může být také klasická či kvantová) a obecně kupy zjednodušujících předpokladů. Feynman (a asi nejen on) tomu říká něco jako "hledání vhodného modelu situace" - a tenhleten model určitě nemůžeme považovat za odvození v matematickém smyslu, spíš jej musíme experimentálně ověřovat.
Ten popis, proč v kovech platí ohmův zákon je určitě dobrý, ale já třeba nevím, proč neplatí i v elektrolytech. Vzdálenost mezi srážkami na napětí tam také záviset nebude, a počet nabitých částic tam bude také pořád stejný.
Dále bych si netroufl odhadnout, jestli platí i v polovodičích.
Offline
#14 28. 02. 2019 05:02 — Editoval KennyMcCormick (28. 02. 2019 05:04)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Ohmův zákon - napětí
Podle mě je spíš trik v tom Pauliho principu - prostor mezi atomovými jádry je "vyplněn" (z hlediska Pauliho prinicipu) elektrony s nízkou energií, takže už se tam žádný další nevejde a jádra se nemohou dostat blíže k sobě .... ale pro elektrony s vyšší energií je tam místa kupa.
Mhm... ale to nevysvětluje, proč se elektron sráží s atomy méně, než by měl? Protože vodivostní elektrony mají větší energii než elektrony stabilně umístěné v orbitalech, jak píšeš, takže by Pauliho princip neměl elektronům vadit?
Ale zase na druhou stranu, teď si uvědomuju, že Pauliho princip platí obecně - i pro elektrony, které nemají přesně stejnou energii - např. jim částečně brání při pohybu vodičem, což není určitě způsobené tím, že by elektron nemohl zaujmout stejnou polohu jako jiný elektron s přesně stejnou energií.
Takže to (z nějakého důvodu) bude asi způsobené i Pauliho principem (který by se možná mohl formulovat nějak semiklasicky... (bez vlnových funkcí)).
Ale pokud já vím, tak skoro všechny vlastnosti látek (zejména pevných) se odvozují zkombinováním klasické fyziky, kvantové mechaniky a statistické mechaniky (ta může být také klasická či kvantová) a obecně kupy zjednodušujících předpokladů. Feynman (a asi nejen on) tomu říká něco jako "hledání vhodného modelu situace" - a tenhleten model určitě nemůžeme považovat za odvození v matematickém smyslu, spíš jej musíme experimentálně ověřovat.
To bude asi pravda.
Já jsem to myslel ve smyslu, že nemusíme Ohmův zákon postulovat jako empirický fakt, ale postulujeme něco, z čeho se potom dá odvodit.
Striktně vzato nemůžeme asi odvodit v klasickém elektromagnetismu nic, co vyžaduje cokoliv jiného než elektromagnetické vlny - a to ještě musejí mít tak velkou intenzitu, aby se neprojevila existence fotonů.
já třeba nevím, proč neplatí i v elektrolytech
V elektrolytech se Ohmův zákon odvodí jinak proto, že:
1. V elektrolytech existuje třecí síla mezi kapalinou a ionty (tohle by se asi dalo odvodit i jako interakce s individuálními částicemi kapaliny, jenomže by to bylo asi komplikovanější, protože v kovu kladné ionty zůstávájí na místě, zatímco molekuly kapaliny mění svoje rovnovážné polohy extrémně rychle).
2. Ionty se pohybují rovnoměrným pohybem po celé cestě, ne rovnoměrně zrychleným se srážkami (tohle by šlo určitě popsat i bez rovnoměrného pohybu, ale otázka je, jak komplikovaně).
3. Ionty nemusejí mít obecně stejný náboj jako elektrony.
Ale na konci zase dojdeme k tomu, že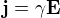 .
.
Ale to neplatí pro silná elektrická pole, a taky nevím, proč.
Dále bych si netroufl odhadnout, jestli platí i v polovodičích.
V polovodičích jsou porušené předpoklady:
1. Nosiče náboje se pohybují nejen díky vnějšímu elektrickému poli, ale i kvůli nestejnoměrné hustotě nosičů náboje (takže vzniká difúzní proud).
2. Neplatí, že střední volná dráha je konstanta nezávisející na směru a poloze nosiče náboje.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#15 28. 02. 2019 08:26
Re: Ohmův zákon - napětí
KennyMcCormick napsal(a):
Ale zase na druhou stranu, teď si uvědomuju, že Pauliho princip platí obecně - i pro elektrony, které nemají přesně stejnou energii - např. jim částečně brání při pohybu vodičem, což není určitě způsobené tím, že by elektron nemohl zaujmout stejnou polohu jako jiný elektron s přesně stejnou energií.
Takže to (z nějakého důvodu) bude asi způsobené i Pauliho principem (který by se možná mohl formulovat nějak semiklasicky... (bez vlnových funkcí)).
Údajně je to tak, že když by byla krystalická mřížka zcela pravidelná (ideální monokrystal, bez poruch), tak se budou elektrony pohybovat krystalovou mříží zcela bez odporu. Ono jim nevadí, že jim atomy stojí v cestě, vadí jim, když se při srážce změní směr jejich rychlosti (hybnosti). A k tomu v pravidelné mřížce nedochází. K rozptylům dochází na nehomogenitách v krystalové mříži - a to mohou být jednak ty strukturální poruchy, a jednak (aspoň se to předpokládá, netuším, jestli to někdy někdo matematicky řešil) nehomogenity vyvolané tepelnými kmity té krystalové mřížky.
Lze to matematicky demonstrovat na zjednodušeném modelu, kdy máme řadu atomů, mezi kterými přeskakuje ten elektron - a na každém atomu má nějakou potenciální energii (vazebnou energii) - a u jednoho z atomů ji má jinou. Potom lze ukázat, že vlna, která rovnici řeší, se na tom jednom atomu částečně odráží. Při troše hraní to lze ukázat i ve 3D prostoru - tam se zase část rovinné dopadající vlny mění na rozptýlenou sférickou vlnu.
KennyMcCormick napsal(a):
Já jsem to myslel ve smyslu, že nemusíme Ohmův zákon postulovat jako empirický fakt, ale postulujeme něco, z čeho se potom dá odvodit.
Jo, to je jasné. Jde jen o to, že aby takovýto postup dával smysl, měl by ten předpoklad, který postulujeme, být nějaký "jednodušší", mít obecnější platnost.
Protože třeba existují obdobná klasická "odvození" jevu zvaný diamagnetismus, a přitom jsou všechna chybná - což lze ukázat už v rámci té klasické teorie.
KennyMcCormick napsal(a):
Striktně vzato nemůžeme asi odvodit v klasickém elektromagnetismu nic, co vyžaduje cokoliv jiného než elektromagnetické vlny - a to ještě musejí mít tak velkou intenzitu, aby se neprojevila existence fotonů.
Jenže tohle platí o čemkoliv. Představa, že vezmeme fundamentální rovnice (ať už jsou to ty Newton-Maxwellovy, nebo rovnice kvantové elektrodynamiky) a pouhou jejich aplikací na každou částici systému odvodíme vlastnosti čehokoliv (parního stroje, počítače, člověka) - takovou představu mohou mít snad jen filozofové. Reálně to takto nefunguje.
KennyMcCormick napsal(a):
Dále bych si netroufl odhadnout, jestli platí i v polovodičích.
V polovodičích jsou porušené předpoklady:
1. Nosiče náboje se pohybují nejen díky vnějšímu elektrickému poli, ale i kvůli nestejnoměrné hustotě nosičů náboje (takže vzniká difúzní proud).
2. Neplatí, že střední volná dráha je konstanta nezávisející na směru a poloze nosiče náboje.
A já bych zrovna řekl, že u polovodiče by to platit mohlo. Já každopádně myslel jen homogenní polovodič, né PN přechod. A proč by střední volná dráha neměla záviset na směru ? Kvůli tomu, že je krystal anizotropický ?
Offline
#16 02. 03. 2019 05:01
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Ohmův zákon - napětí
Údajně je to tak, že když by byla krystalická mřížka zcela pravidelná (ideální monokrystal, bez poruch), tak se budou elektrony pohybovat krystalovou mříží zcela bez odporu. Ono jim nevadí, že jim atomy stojí v cestě, vadí jim, když se při srážce změní směr jejich rychlosti (hybnosti). A k tomu v pravidelné mřížce nedochází. K rozptylům dochází na nehomogenitách v krystalové mříži - a to mohou být jednak ty strukturální poruchy, a jednak (aspoň se to předpokládá, netuším, jestli to někdy někdo matematicky řešil) nehomogenity vyvolané tepelnými kmity té krystalové mřížky.
Lze to matematicky demonstrovat na zjednodušeném modelu, kdy máme řadu atomů, mezi kterými přeskakuje ten elektron - a na každém atomu má nějakou potenciální energii (vazebnou energii) - a u jednoho z atomů ji má jinou. Potom lze ukázat, že vlna, která rovnici řeší, se na tom jednom atomu částečně odráží. Při troše hraní to lze ukázat i ve 3D prostoru - tam se zase část rovinné dopadající vlny mění na rozptýlenou sférickou vlnu.
Takže když se bude vlnová funkce elektronu odrážet od částic v ideální krystalické mřížce, tak výsledkem je vlnová funkce odpovídající elektronu, jehož směr hybnosti se srážkou nemění?
Zase na druhou stranu, to vysvětluje, proč v limitě nulové termodynamické teploty je odpor některých kovů nulový.
to mohou být jednak ty strukturální poruchy, a jednak (aspoň se to předpokládá, netuším, jestli to někdy někdo matematicky řešil) nehomogenity vyvolané tepelnými kmity té krystalové mřížky
Měly by to být i tepelné kmity, aby s rostoucí teplotou rostl odpor.
Protože třeba existují obdobná klasická "odvození" jevu zvaný diamagnetismus, a přitom jsou všechna chybná - což lze ukázat už v rámci té klasické teorie.
Ano, je to tak.
Reálně to takto nefunguje.
Ano, já vím. 🙂
Já každopádně myslel jen homogenní polovodič, né PN přechod.
U homogenního polovodiče jsem nevěděl, jestli platí Ohmův zákon, ale teď jsem si našel, že platí, takže tam ty předpoklady asi můžou být splněny.
A proč by střední volná dráha neměla záviset na směru ? Kvůli tomu, že je krystal anizotropický ?
U homogenního polovodiče asi proto.
Já jsem si představoval úplně libovolný polovodič, kde to může záviset na směru (třeba proto, že je v různých místech různá koncentrace nábojů nebo může být blízko přechod).
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#17 03. 03. 2019 21:38
Re: Ohmův zákon - napětí
KennyMcCormick napsal(a):
Takže když se bude vlnová funkce elektronu odrážet od částic v ideální krystalické mřížce, tak výsledkem je vlnová funkce odpovídající elektronu, jehož směr hybnosti se srážkou nemění?
No ano...
A není na to potřeba ani kvantová mechanika, úplně stejně to funguje i s klasickou el. mag. vlnou. Pokud si atom představíme jako lineární oscilátor ("elektron na pružině").
Původní el. mag. vlna nám tedy rozkmitá všechny ty "elektrony na pružině" - a každý z nich vyzařuje sférickou vlnu do svého okolí. Pak se všechny ty vlny nazvájem vyruší, a zůstane jen ta původní.
No - je tu jedna drobnost, tohle by platilo, kdyby elektron kmital se stejnou fází jako ta dopadající vlna. Jenže to obecně nenastane a kmity elektronu (jakož i jejich vyzářené vlny) mají fázový posuv. A projevuje se to tak, že to sníží fázovou rychlost té původní vlny (tím, že se to k ní přičte). Je to to, co známe jako index lomu. No - za jistých okolností to může fázovou rychlost vlny i zvýšit, ale to nastává jen pokud se trefíme kolem rezonančního kmitočtu těch "elektronů na pružině". Pokud do toho "elektronu na pružině" doplníme i tlumení, tak tam nastává i útlum té postupné vlny, a mám pocit že i její disperze (že se její část všesměrově rozptyluje - že se ty rozptýlené vlny navzájem nevyruší, protože od vzdálených atomů už se tam ta vlna nedostane).
Je to jeden z mála klasických modelů atomů, co docela dobře funguje - alespoň tady na ty věci kolem el. mag. vln procházejících materiály.
Funguje to tak ovšem jen pokud jsou vzdálenosti mezi těmi oscilátory pravidelné. Pokud jsou náhodné (kapičky vody v mlze), tak se to chová jinak, celkem to pěkně rozptyluje.
KennyMcCormick napsal(a):
Zase na druhou stranu, to vysvětluje, proč v limitě nulové termodynamické teploty je odpor některých kovů nulový.
Při absolutní nule by podle mě neměly být v materiálu žádné volné elektrony, které by vedly proud.
Ale to nevím. Každopádně - pokud máš na mysli supravodivost, tak tam je princip docela jiný - totiž ten, že skrze kmity krystalové mříže dokáží dva elektrony vytvořit vázanou strukturu, takovou kvazi-částici, která má celočíselný spin, a chová se tudíž jako boson, takže pro ni neplatí ten pauliho princip, a ostatní elektrony jí nepřekáží v cestě. A vůbec nevadí, že ta částice je mnohokrát větší, nežli jsou vzdálenosti mezi atomy.
KennyMcCormick napsal(a):
to mohou být jednak ty strukturální poruchy, a jednak (aspoň se to předpokládá, netuším, jestli to někdy někdo matematicky řešil) nehomogenity vyvolané tepelnými kmity té krystalové mřížky
Měly by to být i tepelné kmity, aby s rostoucí teplotou rostl odpor.
No to já vím, že by měly, ale chtělo by to nějak doložit že to tak je, né jen tím, že to potřebujeme do naší představy. Ale já to samozřejmě nerozporuji.
KennyMcCormick napsal(a):
Já jsem si představoval úplně libovolný polovodič, kde to může záviset na směru (třeba proto, že je v různých místech různá koncentrace nábojů nebo může být blízko přechod).
To co zmiňuješ, to je spíš nehomogenita.
Ale monokrystaly látek mohou (ale také nemusejí) vykazovat i skutečně anizotropní vlastnosti. Jako že světlo se v nich šíří v každém směru jinak rychle. Závisí to na geometrii té krystalové mřížky.
Pokud jde o vodivost - při kvantovém popisu elektronu pomocí rovinné vlny získáme něco, co se jmenuje "efektivní hmotnost elektronu" - a ač je zhruba stejného řádu, je trochu jiná nežli skutečná hmotnost elektronu ve vakuu. A v anizotropních látkách tahle efektivní hmotnost závisí na směru.
Offline
#18 04. 03. 2019 23:14
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Ohmův zákon - napětí
Při absolutní nule by podle mě neměly být v materiálu žádné volné elektrony, které by vedly proud.
V klasické fyzice by (nejen) v kovu nebyly, ale ve skutečnosti v kovu podle mě budou, protože počet volných elektronů v kovu na jednotku objemu je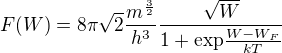 , kde
, kde  je energie elektronu a
je energie elektronu a  je Fermiho mez daného kovu a pro
je Fermiho mez daného kovu a pro  je výsledek větší než 0 i pro
je výsledek větší než 0 i pro  .
.
Každopádně - pokud máš na mysli supravodivost, tak tam je princip docela jiný - totiž ten, že skrze kmity krystalové mříže dokáží dva elektrony vytvořit vázanou strukturu, takovou kvazi-částici, která má celočíselný spin, a chová se tudíž jako boson, takže pro ni neplatí ten pauliho princip, a ostatní elektrony jí nepřekáží v cestě.
Ano.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#19 05. 03. 2019 08:25
Re: Ohmův zákon - napětí
Jo jo, jsem taky vůl ... kovy přece při nízkých teplotách nepřestanou vodit...jen odpor přestává záviset na teplotě.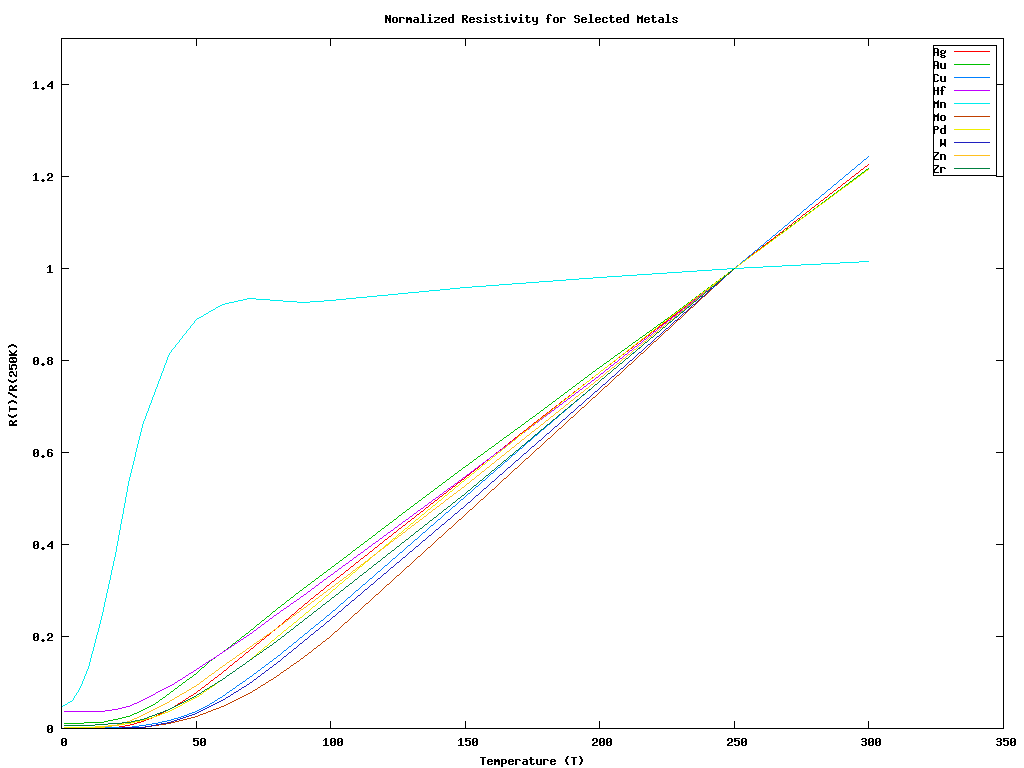
Ale jinak je to dost složitá problematika a vystupuje tam dost vlivů - obrázek pochází odtud, kdyby tě to zajímalo.
Ty hodnoty odporu kolem nuly jsou sice malé (jsou uvedeny v tabulce na začátku odkazovaného článku), ale pořád to ještě není supravodivost. Supravodivé materiály (I. druhu) mají odpor v podstatě nulový.
Offline
#20 09. 03. 2019 00:52
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Ohmův zákon - napětí
Aha, takže z toho, co tam píšou, se zdá, že i v dokonalé mřížce se elektrony s tou mřížkou můžou srážet - např. rozptyl elektronů na variacích spinu (odstavec "Localized Magnetic Electrons") (ať už to funguje jakkoliv). Zase na druhou stranu, možná bychom měli říct, že ta mřížka tím pádem není dokonalá, protože tam je něco, s čím se elektrony mohou srážet. Takže to jsou tyhle "nedokonalosti" v mřížce, které způsobují reziduální rezistivitu?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
