Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 03. 2019 23:06 — Editoval matge (05. 03. 2019 23:08)
Délka křivky vodorovného vrhu
Zdravím, mám určit délku křivky vodorovného vrhu přes integrál, avšak nevím si s ním rady. Je zadán parametricky

s tím, že dopadne do vzdálenosti h, tedy meze jsou <0, h>
vím, že pro délku křivky platí
Stačí mi toto pouze zderivovat a dosadit? Derivuji to podle t. Nebo je nutno to převést na polární souřadnice? To ovšem nevím jak.
Díky
Offline
#4 06. 03. 2019 07:24
#5 06. 03. 2019 11:00
Re: Délka křivky vodorovného vrhu
↑ matge:
Ahoj. Jen doplňující poznámka:
U integrálů - zejména ve fyzice - je v zájmu přehlednosti výhodné specifikovat integrační proměnnou.
V této úloze se integruje podle časové proměnné (protože rychlost v okamžiku  je derivací délky
je derivací délky
"již vykonané" dráhy podle času, takže celková délka dráhy je - stručně řečeno - integrálem rychlosti
podle času). Časovou proměnnou obvykle značíme symbolem  , tudíž příslušný integrál zapíšeme
, tudíž příslušný integrál zapíšeme
ve tvaru
 .
.
Offline
#6 06. 03. 2019 11:38
Re: Délka křivky vodorovného vrhu
↑ Rumburak:
Díky,
tak když zderivuji a dosadím, potom v integrálu mě to vede na substituci. Tam ale nevím co vysubstituovat, protože ani jedna strana mě nikam nevede
Offline
#7 06. 03. 2019 12:52
Re: Délka křivky vodorovného vrhu
↑ matge:
Tento integrál je sestaven správně. K jeho výpočtu lze (po vhodné úpravě) použít jednu z "hyperbolických"
substitucí - pomocí vztahu  . (Funkce sinh , cosh se nazývají hyperbolický sinus,
. (Funkce sinh , cosh se nazývají hyperbolický sinus,
hyperbolický kosinus - zkus se na ně zaměřit, základní vlastnosti by měly stačit. )
Offline
#8 06. 03. 2019 13:20
Re: Délka křivky vodorovného vrhu
↑ Rumburak:
Díky za radu, ale nemůžu přijít na to, jak to vhodně upravit a aplikovat. S hyperbolickými funkcemi jsem se prakticky nikdy nesetkal.
Offline
#9 06. 03. 2019 14:20 — Editoval Honzc (06. 03. 2019 14:25)
Re: Délka křivky vodorovného vrhu
↑ matge:
Parametrické rovnice opravdu odpovídají vodorovnému vrhu. Ovšem ty píšeš, že h je vzdálenost dopadu, ale normálně je to výška nad povrchem odkud se vrh provádí. (čemuž odpovídá i rovnice pro y(t))
Pokud si se spletl a je to opravdu výška, pak meze integrálu budou 
Nápověda:
Např. pro v0=10 ms-1,g=10 ms-2,h=5 m vyjde délka 11.478 m jak výpočtem, tak i modelováním.
Offline
#10 06. 03. 2019 14:37 — Editoval Rumburak (08. 03. 2019 15:10)
Re: Délka křivky vodorovného vrhu
↑ matge:
Pro libovolné komplexní číslo  značíme
značíme ,
,  .
.
Nás u této úlohy samozřejmě zajímají jen  reálná.
reálná.
Snadno nahlédneme, že v libovolném bodě  platí vztahy
platí vztahy
 ,
,
 ,
,  ,
,
které se Ti pro vhodnou úpravu integrandu a nalezení vhodné substituce pomocí těchto funkcí budou hodit.
Offline
 ,
,  .
.
 a
a  jsou časy. Tj.
jsou časy. Tj. 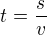 ) ti dá
) ti dá