Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 07. 03. 2019 11:21 — Editoval jardofpr (09. 03. 2019 20:53)
#3 08. 03. 2019 16:36 — Editoval krakonoš (08. 03. 2019 16:51)
Re: Trigonometric Integration
↑ jardofpr:
AHOJ.
Prosim te,muzes mi podrobneji rozepsat jeste tu druhou substituci? Kdyz dosadim za t podle tve substituce,dostavam pod odmocninou -1.
Diky.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#4 08. 03. 2019 17:42 — Editoval jardofpr (08. 03. 2019 17:44)
Re: Trigonometric Integration
ahoj ↑ krakonoš:
predstavoval som si to takto:
![kopírovat do textarea $\int \sqrt{\frac{2-t}{2+t}}\,\frac{\mathrm{d}t}{1+t} = |\mathrm{sub.}| = \int \sqrt{u\bigg[2-\Big(\frac{1}{u}-2\Big)\bigg]}\frac{1}{1+\frac{1}{u}-2}\bigg(-\frac{\mathrm{d}u}{u^2}\bigg) = $](/mathtex/ea/ea772456e409de4d84440cbb96f4bdbe.gif)

vidno to lepšie? (u je teraz z intervalu (1/3,1))
teraz keď na to pozerám asi som sa sekol s mínuskom pred výsledným integrálom
a keď sa v tom vŕtam ďalej tak zisťujem že moja výsledná primitívna funkcia zrejme nie je dobre
postup ktorý som uviedol podľa mňa vedie k cieľu ale niekde som asi urobil chybu lebo moja primitívna funkcia
striedavo rastie a klesá, ale integrovaná funkcia je stále nezáporná
keď budem mať čas sa na to pozriem ale možno to stihneš skôr :)
Offline
#5 08. 03. 2019 18:22 — Editoval krakonoš (08. 03. 2019 23:53)
Re: Trigonometric Integration
↑ jardofpr:
Diky moc.
Stale delam posledni dobou chyby,mam napsano2u-1plus 2u ,a spoctu,ze 2 a2 je 0.
Pri prechodu k treti substituci ti vypadlo minus pred cislem8,se mi zda.
Jestli jsem se nespletla,tak mi vyslo
-2arctg(w) plus 2.sqrt(3).argtgh(w/sqrt3).
Takto vypocteny integral patri intervalu -pi/2,pi/2. V opacnem pripade se musi
dat minus pred prvni integral.
Ja si ten prvni integral odvodila,ze jsem se zbavila odmocniny v citateli rozsirenim zlomku a zvolila substituci za sinus.Pak tam hraje roli signum cosinu,a to je prave to znamenko.Pri tomto postupu ale nesmi byt x rovno pi/2,abychom nedelili nulou.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#7 09. 03. 2019 20:58
Re: Trigonometric Integration
hey ↑ stuart clark:
I edited the original post because of a mistake, should be correct now
ahoj ↑ krakonoš:
urobil som opravu a teraz už sú priebežné integrály správne
vysvetľujem to aj v edite pôvodného príspevku ale chyba bola primárne v spätnom dosadzovaní 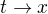
lebo som nerozdelil integrál s premennou  na dva prípady ako to malo byť
na dva prípady ako to malo byť
skúšal som aj tvoj postup a povedal by som že pred arctan-om v tvojom riešení nebude mínus,
inak primitívna funkcia nebude nakoniec na požadovanom intervale rásť
mimo toho to vyzerá fajn, tvoj arctanh je ďalšie vyjadrenie logaritmu v mojom riešení takže to bude tiež dobre
Offline
#8 09. 03. 2019 23:51 — Editoval krakonoš (10. 03. 2019 09:52)
Re: Trigonometric Integration
↑ jardofpr:
Ahoj.
U druheho scitance ve vysledku mi ale misto odmocniny ze3 vysly dve odmocniny ze tri(odmocnina ze tri je ze substituce a ta dvojka vznikla jako6:3,kde sestka byla pred integralem po rozkladu na parcialni zlomky a trojka vznika vytknutim cisla3ze jmenovatele - integral s prom w). Jinak se shodujem.
Jinak obdivuji tvuj uhodnuty rozklad v minulem prikladu(soucty4tych mocnin sin a cos delenosoucty tretich mocnin).Ja si to musela odvodit pomoci tg a cotg.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#9 10. 03. 2019 14:31
Re: Trigonometric Integration
hoj ↑ krakonoš:
tie 2 odmocniny z troch su fajn,
len by si podla mna mala mat  na intervale
na intervale 
inak ti primitivna funkcia klesá na tom intervale
ono po tých substitúciách je 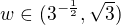 tak sa dá cez taylorov rozvoj napríklad vidieť že
tak sa dá cez taylorov rozvoj napríklad vidieť že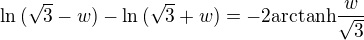 pre w z tohto intervalu
pre w z tohto intervalu
a ďakujem :) najprv som mal samozrejme menovateľ rozložený a potom keď už vieš čo hľadáš tak to nejak ide
Offline
#10 10. 03. 2019 15:01
Re: Trigonometric Integration
↑ jardofpr:
DIKY moc.
Uz to vidim.Pri rozkladu 6/sqr(w)-3 na parcialni zlomky tam fiuruje 1/2 ,takze se to zkrati.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline

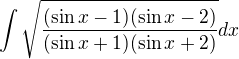
 as of periodicity of the function
as of periodicity of the function
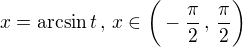
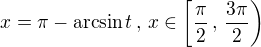
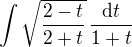

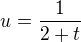 integral becomes
integral becomes 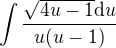
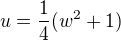 we get
we get 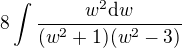
 where
where  for
for 
 same thing as in
same thing as in  sign coming from derivative of
sign coming from derivative of 
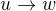 I made numerical mistake)
I made numerical mistake) after substituting backwards there is constant needed to be added on one side of the interval
after substituting backwards there is constant needed to be added on one side of the interval