Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 01. 2013 21:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pravděpodobnost
↑ p.monkk:
Zdravím,
zajímavá úloha :-) Předně - dětí mít nemusíme, dětí mít chceme. Ale v rodině ve Tvé úloze o kluka zas tak moc zájem neměli (skutečně jen 0,99 %?)
kluci i holky se rodí se stejnou pravděpodobností?
moje praktická zkušenost říká, že tomu tak je, ale s ohledem na výsledek Tvé úlohy bych řekla, že pravděpodobnost narození kluka je cca 0,65. Odkud je úloha a čím má být zajímavá, že jsi umístila do sekce Zajímavých úloh? A do které sekce fóra mám přesunout téma? Děkuji.
----------
"Co to znamena "skoro naprosto jisty"? Pripada mi to, jako by se reklo, ze nejaka zena je "tak trochu tehotna"." (c)
Offline
#4 27. 01. 2013 23:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pravděpodobnost
↑ p.monkk:
tak když musíme :-) Zkus se ještě podívat na zadání (zda jsi něco nevynechala), nebo umístí přímo náhled na zadání.
kluci i holky se rodí se stejnou pravděpodobností?
To je v zadání nebo to je Tvůj dotaz?
-----------
"Pokud to není ono, musím znát autora a pak zkusit hledat. Pravděpodobně budu pak schopen najít některou verzi v elektronické podobě." (c)
Offline
deti a pravdepodobnost chlapca je 0.5. Aka je pravdepodobnost, ze to budu vsetko dievcata? Aka je potom pravdepodobnost, ze aspon jeden je chlapec?#6 28. 01. 2013 09:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pravděpodobnost
↑ Brano:
Zdravím,
přesně tak jsem zkoušela (binomické rozdělení, p=0,5, varianty "alespoň jeden chlapec", "pravě jeden chlapec") za použití zadání a nabízeného výsledku od kolegyně:
kolik musíte mít dětí, aby pravděpodobnost, že budete mít kluka byla 0,99 procent. kluci i holky se rodí se stejnou pravděpodobností? (výsledek 7) Dík
musíš uznat, že je značně nepřesné a o výsledku se dá jen debatovat. ↑ příspěvek 2:. Je tak? Děkuji.
----------------------
"S matematikou to určitě souvisí, jen bych poprosil přesné vyjadřování. V opačném případě se to bude řešit těžce a může se stát, že chceš něco úplně jiného, než to, co se zde objeví jako řešení k tvé úloze". (c)
Offline
#7 25. 06. 2013 19:11
Re: Pravděpodobnost
ahoj prosím nutně potřebuji pomoc s příkladem :
V osudí je 15 bílých a 10 černých koulí . Jaká je pravděpodobnost , že při tahu 4 koulí budou 2 bílé a 2 černé ?
Já a matematika to vůbec nejde dohromady ...najde se tu někdo kdo by byl ochotný mi to vypočítat i s postupem abych to nějak pochopila :D děkuji moooooc !!! :)
Offline
#8 25. 06. 2013 21:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pravděpodobnost
↑ kačenka93:
Zdravím,
založ si, prosím, vlastní téma v sekci SŠ, nepiš do cizích témat viz pravidla. A také ne do sekci "Zajímavých".
K vyřešení úlohy by měl pomocí tento materiál. Uvažuj, že celkem v osudí je (15+10) koulí. Jak je pravděpodobnost vytažení černé koule? A Jaká je pravděpodobnost vytažení bílé koule? Úlohu dovršíš stanovením, že musí zároveň nastat situace - při tahu vytáhnu pravě 2 bílé a zároveň pravě 2 černé. Pokud nepomůže, tak si založ nové téma. Děkuji.
Offline
#10 23. 09. 2015 23:32
- klarkavankova
- Zelenáč
- Příspěvky: 1
- Škola: SLU
- Pozice: student
- Reputace: 0
Re: Pravděpodobnost
Zdravím, dnes jsme na hodině pravděpodobnosti dostali za úkol jak se nazývá jev, který je použitý ve známé hře skořápky. Může mi někdo pomoc ? nemůžu to najít nikde :)
Offline
#11 24. 09. 2015 23:49
- check_drummer
- Příspěvky: 5053
- Reputace: 106
Re: Pravděpodobnost
↑ klarkavankova:
Ahoj, nevím jestli to není spíš na jiné téma a taky zda to bude odpověď na tvou otázku, ale jistou analogii vidím v tzv. Monty Hall problému.
"Máte úhel beta." "No to nemám."
Offline
#12 24. 09. 2015 23:56
Re: Pravděpodobnost
↑ klarkavankova:
V realite jav znamy ako podvod. Ale zakladaj si vlastne temy.
Offline
#13 25. 09. 2015 06:30
Re: Pravděpodobnost
↑ klarkavankova:
Zkus si přečíst Toto
↑ check_drummer:
Zdravím,
u Monty Hall problému jde asi o trochu něco jiného.
Offline
#16 26. 09. 2015 23:36
- check_drummer
- Příspěvky: 5053
- Reputace: 106
Re: Pravděpodobnost
↑ Brano:
Nevím jak přesně fungují skořápky, ale dle mého jsou tam tři "entity" (skořápky) a uvnitř jedné je ukryta hledaná entita (kulička), přičemž úkolem je uhádnout, kde kulička je. Navíc po provedeném tipu může skořápkář odkrýt jednu ze skořápek - a ukázat, že je prázdná. Takže z tohoto pohledu se mi jeví podobnost velmi velká...
"Máte úhel beta." "No to nemám."
Offline
#17 16. 11. 2017 17:03
Re: Pravděpodobnost
Zdravím, narazil sem na jeden ukázkový úkol, s kterým si nevím úplně rady, mohl by mi prosím pomoct někdo s postupem? Příklad zní :
V rybníce byl proveden odchyt 50 ryb, které byly následně označeny a vypuštěny zpět. Následující den byl proveden nový odchyt 100 ryb. Z těchto 100 ryb bylo 10 označených. Jaká je pravděpodobnost, že v rybníce je přesně 500 ryb?
Offline
#18 17. 11. 2017 03:57
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pravděpodobnost
Ahoj, založ si prosím na svůj příklad nové téma.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
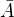- na žádné z kostek nepadne šestka.