Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definiční obor funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 03. 2019 17:26
Definiční obor funkce dvou proměnných
Dobrý den, máme určovat definiční obory funkcí dvou proměnných pomocí obrázku. Moc mi to nejde, snažím se ale vždycky někde udělám chybu.
Mám příklad:
Rozebral sem si to na části a nakreslil sem grafy.
x = přímka procházející počátkem = parabola na ose y
= parabola na ose y
jako definiční obor sem určil průsečík tady těch dvou grafů, ale nejsem si jistý jestli je to správně. Obrázek bohužel nenahraju, zapomněl jsem si doma kabel k mobilu a nemám tu wifi na mobil.
Offline
- (téma jako vyřešené označil(a) NeuRotiCk)
#2 25. 03. 2019 18:36 — Editoval Sherlock (25. 03. 2019 18:39)
Re: Definiční obor funkce dvou proměnných
To rozebrání na části mi nedává žádný smysl. Např.  je proměnná, ne přímka... přímka bývá popsána rovnicí a ne jedním výrazem/proměnnou.
je proměnná, ne přímka... přímka bývá popsána rovnicí a ne jedním výrazem/proměnnou.
---
Zkus na to jít jinak: jaké hodnoty  a
a  můžeš dosadit do výrazu
můžeš dosadit do výrazu  , aby dával smysl?
, aby dával smysl?
Offline
#7 25. 03. 2019 19:07
Re: Definiční obor funkce dvou proměnných
Kdyby to byl jen ten první, znamenalo by to že definiční obor jsou takové dvojice 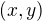 , že
, že  a
a 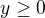 .
.
Offline
#9 26. 03. 2019 14:10
Re: Definiční obor funkce dvou proměnných
Ahoj ↑ NeuRotiCk:,
↑ Sherlock: ti velmi pomohol, preco mu nedas + do reputacii?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definiční obor funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)

 a definiční obor je podmnožina
a definiční obor je podmnožina  , tedy v def. oboru jsou
, tedy v def. oboru jsou 