Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 03. 2019 17:02
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Báze duálního prostoru
Dobrý den,
je li báze duálního vektorového prostoru 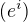 indukovaná bází
indukovaná bází 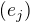 definována vztahem
definována vztahem 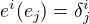 , znamená to, že k ortonormální bázi
, znamená to, že k ortonormální bázi 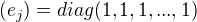 má báze duálního prostoru stejné prvky a tedy složky (souřadnice) vektoru a kovektoru jsou stejné?
má báze duálního prostoru stejné prvky a tedy složky (souřadnice) vektoru a kovektoru jsou stejné?
Díky.
Petr
Offline
#2 26. 03. 2019 17:54
Re: Báze duálního prostoru
Ahoj.
Duální baze nemůže mít stejné prvky. Jedno jsou vektory a druhé formy.
složky (souřadnice) vektoru a kovektoru jsou stejné?
Jak se definuje kovektor k danému vektoru?
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 26. 03. 2019 21:03
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Báze duálního prostoru
Neřeším jak jsou prvky uspořádané, ale jen že by měli být stejné, aby platila definice duální báze přes Kroneckerovo delta. Jaká je tedy duální báze k bázi 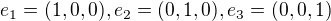 ? Není stejná akorát každý bázový vektor je transponovaný?To samé tedy i pro složky (souřadnice)? To jestli píšeme vektory do řádku nebo do sloupce je jen otázkou konvence a definice skalárního součinu, ne? Nejsou kontravariantní a k nim duální kovariantní tenzory, tedy např. lineární formy a vektory, stejnými invariantními objekty jen v jiných bázích?
? Není stejná akorát každý bázový vektor je transponovaný?To samé tedy i pro složky (souřadnice)? To jestli píšeme vektory do řádku nebo do sloupce je jen otázkou konvence a definice skalárního součinu, ne? Nejsou kontravariantní a k nim duální kovariantní tenzory, tedy např. lineární formy a vektory, stejnými invariantními objekty jen v jiných bázích?
Offline
#4 26. 03. 2019 21:49 — Editoval Andrejka3 (26. 03. 2019 21:52)
Re: Báze duálního prostoru
Takže vektory zapisujete asi takhle
a formy
tak, aby  .
.
Pak přiřadit 
znamená buďto použít přirozený izomorfismus prostoru a jeho duálu 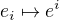 , nebo využít nějakého skalárního součinu
, nebo využít nějakého skalárního součinu 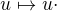 . Druhý pohled se shoduje s prvním, když jsi v ON bazi.
. Druhý pohled se shoduje s prvním, když jsi v ON bazi.
No a víc asi ze mě nedostaneš, protože mluvíme jiným jazykem, tak snad někdo jiný pomůže.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 26. 03. 2019 22:03
Re: Báze duálního prostoru
↑ Roscelinius:
Ahoj, jestli si dobre pamatuju tak k bazi 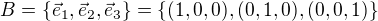 je dualni baze
je dualni baze 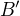 tvorena linearnimi formami
tvorena linearnimi formami 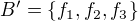 , kde
, kde 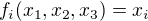 . Souradnice kazde z bazovych forem vzhledem k bazi
. Souradnice kazde z bazovych forem vzhledem k bazi 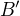 jsou pak samozrejme
jsou pak samozrejme ![kopírovat do textarea $[f_i]_{B'}=\vec{e}_i$](/mathtex/71/7115b191d64ede9e683d879c520ae55b.gif) .
.
Myslim, ze (zvlaste) fyzikove radi pouzivaji zkratku a vynechavaji fakt, ze se jedna o souradnice vzhledem k bazi.
Na druhou stranu lze jejich pocinani opodstatnit pouzitim Rieszovy vety o reprezentaci funkcionalu:
Kazdou linearni formu 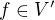 lze totiz jednoznacne reprezentovat prvkem
lze totiz jednoznacne reprezentovat prvkem 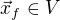 tak, ze
tak, ze 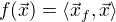 . Namisto
. Namisto  tedy staci pocitat s
tedy staci pocitat s 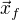 .
.
Pro linearni formy 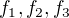 pak tedy plati
pak tedy plati 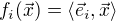 .
.
Offline
#6 26. 03. 2019 22:07
Re: Báze duálního prostoru
Riezsova veta zde neni potreba- jsme jen v konecne dimenzi. Vsechny spojite funkcionaly na R^n se daji reprezentovat pomoci vektoru, pricemz dualita je reprezentovana skalanim soucinem. Pro tvou konkretni (kanonickou) bazi samozrejme dostanes tu samou bazi dualniho prostoru, ponevadz 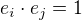 prave kdyz
prave kdyz  .
.
Offline
#7 27. 03. 2019 07:28
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Báze duálního prostoru
Sice asi ukážu, že jsem toho ještě hodně nepochopil, ale jaký má smysl zavádět lineární formy, když vždy mohu v konečných prostorech nalézt ortonormální bázi, která je stejná jak ta k ní duální? Proč nejde vnější algebra vystavět na vektorech? Díky
Offline
#8 27. 03. 2019 15:22
Re: Báze duálního prostoru
Ahoj ↑ Roscelinius:,
Poznamka.
Mozno tu najdes dalsie uzitocne informacie
https://en.m.wikipedia.org/wiki/Dual_basis
https://fr.m.wikipedia.org/wiki/Base_duale
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 27. 03. 2019 15:23
Re: Báze duálního prostoru
↑ Roscelinius:
Když se o tom nebude mluvit, neznamená to, že to tam nebude. Podle mě je občas třeba znát hodnotu skalárního součinu dvou vektorů (číslo) a to někdy představuje důležitý fyzikální invariant (co si matně vybavuju). Ale skalární součin sám o sobě je bilineární forma a když už se mu dá jeden vektor a čeká na druhý, jedná se o lineární formu.
Ve fyzice jsou fajn odpovídatelé, kteří rádi píší o str lidem, kteří nejsou lidoví myslitelé. Třeba by stálo za to se ptát tam.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 27. 03. 2019 17:37
Re: Báze duálního prostoru
Ahoj ↑ Roscelinius:,
Len tak pre zaujimavost:
Dokazes najst dualnu bazu tejto
e1 = (1, 1, 1), e2 = (1, 0, −1) a e3 = (0, 1, 1).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 27. 03. 2019 17:43
Re: Báze duálního prostoru
Roscelinius napsal(a):
Sice asi ukážu, že jsem toho ještě hodně nepochopil, ale jaký má smysl zavádět lineární formy, když vždy mohu v konečných prostorech nalézt ortonormální bázi, která je stejná jak ta k ní duální? Proč nejde vnější algebra vystavět na vektorech? Díky
Já si nejsem úplně jistý, jestli to, co tu řešíte je přesně to, co mám na mysli já - totiž kontravariantní a kovariantní vektory, ale přijde mi, že je to to samé.
No a - ono by to asi velký smysl nemělo, zavádět tyhle dva druhy vektorů, kdybychom počítali jen v euklidovských prostorech (s jednotkovou metrikou). Ale význam to získá v prostorech obecnějších.
Například když budeme používat jiné druhy souřadnic - třeba polární, sféricky atd... Potom už musíme rozlišovat, jestli je daný vektor kontravariantní nebo kovariantní - ony se jinak mění při změně souřadnic.
Pokud třeba máme parametrickou rovnici nějaké čáry (trajektorie) v prostoru, tj funkce 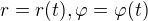 , tak vektor rychlosti
, tak vektor rychlosti 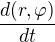 je kontravariantním vektorem.
je kontravariantním vektorem.
Pokud naopak budeme mít vektor vytvořený jako gradient nějaké skalární funkce 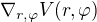 , tak je tento vektor kovariantní.
, tak je tento vektor kovariantní.
Pokud bychom třeba jen měnili měřítka os (osy r, u  to moc nejde), bude se jeden z vektorů zvětšovat, a druhý zmenšovat.
to moc nejde), bude se jeden z vektorů zvětšovat, a druhý zmenšovat.
Pokud už máme vektor jako 2 (3, 4, ...) čísla, tak už to nepoznáme, jestli je to kontravariantní nebo kovariantní. Musíme to vědět předtím, musíme vědět, jak jsme vektor vytvořili nebo definovali.
Další použití těchto věcí je samozřejmě v zakřivených, neeuklidovských prostorech (tenzory na varietě) - tam se křivočarým souřadnicím nevyhneme. A tento aparát využívá obecná teorie relativity.
Pravda je, když nad tím tak přemýším, že vlastně nevím, zdali je třeba intenzita elektrického pole E kontravariantní nebo kovariantní vektor. Nikdy jsem Maxwellovy rovnice v polárních souřadnicích neřešil...
Offline
#12 27. 03. 2019 17:57
Re: Báze duálního prostoru
Totiž - v kartézských souřadnicích se nemusíme příliš starat o to, že pro vektor potřebujeme bázi vektorového prostoru zatímco pro souřadnici bodu, ve kterém se ten vektor nachází, vlastně ani žádnou bázi nepotřebujeme.
Když máme osy X, Y, Z tak je považujeme za bázi všech vektorů, co se v tom prostoru nacházejí, a zároveň za "bázi" všech bodů, co tam jsou. Je to tak samozřejmé, že se nad tím skoro nikdo ani nezamyslí.
Jenže u křivočarých souřadnic musíme zavést bázi pro vektory tak, aby byla v každém bodě "tečná k souřadným osám", tj např. k  u polárních souřadnic. Báze se tak bod od bodu mění ("zvětšuje", "otáčí", "svírá"), a to se nám samozřejmě projeví, pokud podle takovýchto souřadnic derivujeme.
u polárních souřadnic. Báze se tak bod od bodu mění ("zvětšuje", "otáčí", "svírá"), a to se nám samozřejmě projeví, pokud podle takovýchto souřadnic derivujeme.
A proto potřebujeme dva druhy vektorů - jedny které se chovají jako souřadnice, a druhé, které se chovají jako derivace podle těchto souřadnic.
Ale jinak - na tohle nejsem žádný odborník, tak to berte s rezervou...
Offline
#13 27. 03. 2019 18:10
Re: Báze duálního prostoru
Jestli tomu dobře rozumím (což v tomto případě vůbec nemusí být pravda)...
Byla tu zmínka o skalárním součinu. Skalární součin dvou vektorů musí vyjít stejný bez ohledu na to, v jakých souřadnicích vektory reprezentujeme. Skalární součin je skalár, jeho velikost závisí jen na poloze v prostoru. Je to jen číslo.
Pokud tedy máme dva vektory v kartézských souřadnicích, a ty samé vektory vyjádřené třeba v polárních souřadnicích, musí jejich skalární součin vyjít stejný. Proto můžeme dělat skalární součin "napřímo" jen mezi kontravariantním a kovariantním vektorem, a jinak do toho musíme vložit ještě metrický tenzor. Aspoň teda myslím, že to tak je.
Z čehož také plyne, že né každé číslo "umístěné do prostoru" musí být nutně skalárem. Například jedna ze souřadnic vektoru není sama skalárem.
Offline
#14 27. 03. 2019 18:23
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Báze duálního prostoru
↑ vanok:
Řekl bych, že je to 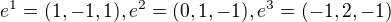 .
.
Offline
#15 27. 03. 2019 20:43 — Editoval vanok (28. 03. 2019 05:36)
Re: Báze duálního prostoru
Ahoj ↑ Roscelinius:,
Ano je to tak....ale transpozovane.
Spomienky na kovariantne vektory a kontravariantne mam z master (mecaniky) a iste ste to videli ako <| ...... |> ( to sa cita: bra.....ket). Myslim si ze sa to vidi aj v kvantovej fyzike.
V podstate ide o oznacenia...
Co sa tyka vseobecne takych problemov. Sluzia v matematike na suvisi medzi morfizmamy a ich transpozovanych. Ako aj väzby medzi podpriestormy a ich otrogonalnymi. Podobne aj medzi jadrami a obrazmi. .... tiez treba dobre vediet pouzivat dualitu. ( ako napr aj pojem diiferencialu realnej funkcie). Napada ma v rychlosti napr. ze pojem urciteho integralu, ci Lagrangeovych polynomov ... lin. formy.
Uzitocne je si prestudovat aspon odkazy co som napisal vyssie . A pochopitelne kazdy, co ma pouzivat taketo pojmy, by mal si prestudovat  linearnu algèbru na dostatocnej urovni.
linearnu algèbru na dostatocnej urovni.
( poznamka: tu som hovoril len o konecnej dim. )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
