Matematické Fórum

gestapák · 26. 03. 2019 19:23

Čau, mám tady trochu problém:

Máme střídavý RL obvod, kde je napětí zdroje . Potom pro proud v ustáleném stavu platí ,

kde třeba , jak to vyplývá z fázorového řešení.

Pro obvod platí dif. rovnice:

Z (2) playne a když už znám proud podle (1), stačí derivovat, dosadit za a potom by mělo platit ne? Jenomže to neplatí. Nemusím to ani zkoušet obecně upravovat, když si nechám v Desmosu vykreslit grafy, tak ty grafy se pro libovolné hodnoty parametrů vůbec nepřekrývají. Funguje to jenom pro případ, kdy R=0 (a tam je to jednoduchá úprava).

Ale když řeším rovnici (3), dostanu výraz:
. Tohle řešení jsem dostal z Wolframu. Jestli to chápu správně, tak člen vyjadřuje přechodnost děje a když ho vynechám (v nekonečnu se rovná nule), dostanu tak průběh proudu pro ustálený stav. Pro oba tyto případy doszení do Kirchhoffa funguje podle vykreslených grafů bez problémů a opravdu platí . (I když jsem to obecně neupravoval.)

Navíc i s vynechaným "členem přechodnosti" podle vykreslených grafů neplatí rovnost

Tak teda nevím, co s tím. Všechno jsem několikrát kontroloval a myslím, že tam žádná matematická chyba není. Může mi na to někdo posvítit? A případně vysvělit, jak se od řešení dif. rovnice přejde k výrazu (1) pro fázový posuv proudu?

MichalAld

Rovnice je lepší psát takto: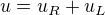

$u=u_{R} + u_{L}$

$U\sin (\omega t)=Ri + L\frac{d}{dt}i$

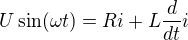
A teď k tvé otázce. Řešení uvedené rovnice sestává (když použiji technický žargon) z ustáleného řešení, a z přechodového děje. Matematici by to nazvali partikulární řešení a obecné řešení.

To obecné řešení (přechodový děj) je řešení rovnice "bez pravé strany", tj.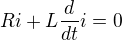

$Ri + L\frac{d}{dt}i = 0$

a v tomto případě (rovnice prvního řádu) je to prostě klesající exponenciála tvaru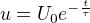

$u=U_0 e^{-\frac{t}{\tau}}$

Řešení, které jsi napsal na začátku, to s těmi sinusovkami, to je to ustálené řešení. Když už přechodový děj odezní. Pokud počítáme pomocí těch fázorů, počítáme vždy JEN USTÁLENÁ ŘEŠENÍ.

Celkové řešení je tedy součtem ustáleného řešení (fázově posunutá sinusovka) a přechodového řešení (ta klesající exponenciála).

No, vhodnou, ale opravdu jen vhodnou volbou počáteční podmínky lze také dosáhnout toho, že tam žádný přechodový děj nebude. Ale ta vhodná volba není i(0) = 0, ta vhodná volba je, když i(o) se rovná proudu, který by tam tekl v ustáleném stavu. Ale je to spíš taková teoretická věc.

Praktický příklad přechodového děje uvedené situace je známý třeba ze silových rozvodů. Když se totiž řeší třeba zkratová odolnost rozvaděčů, musí se brát v úvahu jak ten ustálený (zkratový) proud, kde se berou v úvahu jeho tepelné účinky, a navíc i ten přechodový (zkratový) proud, který může být v nepříznivém případě snad i 2x vyšší, a na něj se zase musí dimenzovat z hlediska jeho mechanických (magnetických) účinků.

MichalAld · 26. 03. 2019 22:14

Jo, a tohle je nějaká blbost, to z ničeho neplyne.

Matematické Fórum

#1 26. 03. 2019 19:23

Proud ve střídavém RL obvodu

#2 26. 03. 2019 22:08 — Editoval MichalAld (26. 03. 2019 22:10)

Re: Proud ve střídavém RL obvodu

#3 26. 03. 2019 22:14

Re: Proud ve střídavém RL obvodu

Zápatí