Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 03. 2019 21:50 — Editoval NeuRotiCk (27. 03. 2019 21:50)
Obsah oblasti ohraničené křivkami
Dobrý den, mám jeden příklad, jen si nejsem jistý jestli jsem dobře spočítal meze:
Vypočítejte obsah oblasti ohraničené křivkami

Grafy mám udělané, nic těžkého to není, parabola se posune do 1 na x-ové ose.
Meze jsem počítal takto:
Prvně jsem si spočítal kořeny té kvadratické a to mě vyšlo 
a pak jsem dosadil za y do první rovnice: 
Z toho vyjdou kořeny: 
Pak by se mi to teda rozpadlo na dva integrály v mezích od 0 do 1 a od 1 do 2.
Horní funkce by byla ta konstantní 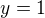 a dolní by byla ta parabola.
a dolní by byla ta parabola.
Počítám správně nebo někde dělám chybu?
Předem děkuji za jakoukoliv odpověď.
Offline
#2 27. 03. 2019 22:18
Re: Obsah oblasti ohraničené křivkami
↑ NeuRotiCk:
Hezký den.
Řekl bych, že postup je v pořádku, jen není důvod dělit integraci na dvě části. Klidně integrovat v mezích od nuly do dvou.
Pokud se tedy nemýlím.
Offline
