Matematické Fórum

teolog · 28. 03. 2019 12:57 — Editoval teolog (28. 03. 2019 12:57)

Zdravím,
řešil jsem úlohu a výsledek uvedený v učebnici mi nesedí s mým postupem. Můžete mi pomoct najít chybu v mém výpočtu nebo potvrdit, že výsledek v učebnici je chybný? Díky

Zadání: V osudí je b bílých a c červených koulí. Táhneme postupně dvě koule, bez vracení do osudí. Nechť B1 značí "v prvním tahu byla tažena bílá koule", B2 značí "v druhém tahu byla tažena bílá koule". Vypočtěte P(B1) i P(B2).

$P(B_1)=\frac{b}{b+c}$ to je jasné

Druhý tah rozdělím na dva případy, podle výsledku tahu v prvním tahu. Pokud jsem jako první vytáhl bílou kouli (a nevrátil jsem ji), je $P(B_2)=\frac{b-1}{b+c-1}$
Pokud jsem v prvním tahu vytáhl červenou kouli (a nevrátil jsem ji), je $P(B_2)=\frac{b}{b+c-1}$
Obě pravděpodobnosti sečtu a dostanu tak celkový výsledek $P(B_2)=\frac{b-1}{b+c-1}+\frac{b}{b+c-1}=\frac{2b-1}{b+c-1}$
V učebnici uvádějí výsledek $P(B_1)=P(B_2)=\frac{b}{b+c}$

Ferdish · 28. 03. 2019 13:38

Mne sa nezdá, že by si mohol jednotlivé pravdepodobnosti javov pri druhom ťahu len tak jednoducho sčítať.

Nech $b=10, c=12$ napríklad.

Pre prvý ťah by potom podľa tvojich úvah platilo $P(B_1)=\frac{10}{22}=0.5$ , čo je OK.

No pre druhý ťah by platilo 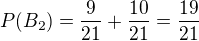$P(B_2)=\frac{9}{21}+\frac{10}{21}=\frac{19}{21}$ , čo mi príde pre danú situáciu ako abnormálne vysoké číslo.

Jj · 28. 03. 2019 14:43

↑ teolog:

Hezký den.

Jak píše kolega, zřejmě trochu jinak. Zkusil bych:

$P(B_2)=P(B_2|B_1)P(B_1)+P(B_2|C_1)P(C_1)=\cdots$

Matematické Fórum

#1 28. 03. 2019 12:57 — Editoval teolog (28. 03. 2019 12:57)

Podmíněná pravděpodobnost

#2 28. 03. 2019 13:38

Re: Podmíněná pravděpodobnost

#3 28. 03. 2019 14:43

Re: Podmíněná pravděpodobnost

Zápatí