Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2019 22:04
Geometrická posloupnost se součtem n členů = 0
Zdravím,
Mám zjistit, jestli je možná aby se součet n členů geometrické posloupnosti, jejíž žádný člen není nula, rovnal nule.
Zkoušela jsem použít vzorec pro součet n členů. Nicméně z celé té rovnice mi vyšlo že n=0, což moc nedává smysl - že součet 0 členů jakékoli posloupnosti se rovná 0, je až příliš evidentní...
Ta posloupnost, u které to platí, by měla být aˇn= (-1)^n. Nicméně nemůžu přijít na to, jak se k tomu předpisu dostat jinak než odhadem a metodou pokus-omyl....
"Když ji miluješ, je pořád co řešit..."
Offline
#2 03. 04. 2019 22:31 — Editoval Ferdish (03. 04. 2019 22:31)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Geometrická posloupnost se součtem n členů = 0
Vážne pre nulový súčet prvých n členov GP vyplýva len jedno riešenie, a síce n=0? Skús sa nad vzťahom, ktorý si úpravami dostala, ešte trochu zamyslieť...
Offline
#3 03. 04. 2019 22:40
Re: Geometrická posloupnost se součtem n členů = 0
No.... Pro q jiné než jedna je součtový vzore: s=a1* (((q^n) -1)/(q-1)). s=0. Ze součinového tvaru vyplývá že buď a1=0 (což je zadáním vyloučeno), anebo ten zlomek = 0. Tedy jeho čitatel=0, a a když q^n=1. n je tedy nula, nebo by to mohla být teoreticky +-1, ale to by pak q muselo být 1, a to není, bo jmenovatel zlomku....
Pro q=1 je vzorec s=a1*n, takže buď a1=0 (nemůže, bo zadání) nebo n=0. A došla jsem tam kde jsem byla celou dobu...
"Když ji miluješ, je pořád co řešit..."
Offline
#5 05. 04. 2019 01:14 — Editoval Ferdish (05. 04. 2019 08:19)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Geometrická posloupnost se součtem n členů = 0
Zrejme treba naznačiť viac...skús si teda miesto toho predstaviť, že kvocient GP je premenná a vlastne riešiš rovnicu 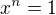 pre n prirodzené a väčšie ako 1.
pre n prirodzené a väčšie ako 1.
Offline
#6 05. 04. 2019 07:51
Re: Geometrická posloupnost se součtem n členů = 0
Ahoj ↑ Ferdish:,
Poznamka.
Ked pises
Odpoveďou na otázku teda je: áno, je možné aby súčin prvých n členov GP bol rovný nule za predpokladu, že n je párne a súčasne kvocient GP q=-1.
To si iste chcel napisat
Odpoveďou na otázku teda je: áno, je možné aby súčet prvých n členov GP bol rovný nule za predpokladu, že n je párne a súčasne kvocient GP q=-1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

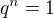 a skús rozlíšiť 2 prípady: párne a nepárne
a skús rozlíšiť 2 prípady: párne a nepárne  .
.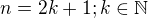 , naša funkcia je prostá, čiže pri odmocňovaní si nemusíme lámať hlavu s absolútnou hodnotou a dostávame
, naša funkcia je prostá, čiže pri odmocňovaní si nemusíme lámať hlavu s absolútnou hodnotou a dostávame 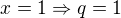 .
.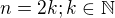 , tu už musíme pri odmocnení brať do úvahy absolútnu hodnotu, teda
, tu už musíme pri odmocnení brať do úvahy absolútnu hodnotu, teda 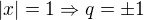 .
.