Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2019 18:01
podmínky pro parametry v rovnici
Dobrý den,
mám zadaný příklad
Uveď podmínky pro parametry v rovnici 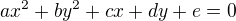 aby dané vyjádření představovalo rovnici hyperboly.
aby dané vyjádření představovalo rovnici hyperboly.
Vím, že pro oba typy hyperboly, bez ohledu na orientaci její osy, platí:
Což pro hyperbolu s hlavní osou rovnoběžnou s osou x znamená:
a hyperbolu s hlavní osou rovnoběžnou s osou y znamená:
a dále jsem našel, že zároveň musí platit podmínka, že: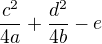 se nerovná nule.
se nerovná nule.
Tuto podmínku dostaneme úpravou počátečního výrazu na čtverec, ale bohužel přes všechnu snahu jsem nepřišel na to, jak to upravit. Prosím o jakoukoli pomoc. Děkuji
Offline
#2 11. 04. 2019 18:16
Re: podmínky pro parametry v rovnici
↑ Varagner:
úprava na čtverec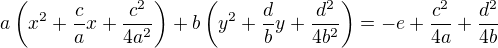
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
