Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 04. 2019 23:28 — Editoval Vojcek1339 (10. 04. 2019 23:57)
- Vojcek1339

- Zelenáč
- Příspěvky: 13
- Reputace: 0
složitější exponenciální rce
![kopírovat do textarea $[2\{2^{\sqrt{x+3}}\}^{\frac{1}{2\cdot \sqrt{x}}}]^{\frac{2}{\sqrt{x}-1}}=4$](/mathtex/40/4091aa92124f8322edbfdaa1c1cfd45d.gif)
potřeboval bych poradit s tímhle příkladem prosím.. pokud možno krok po kroku abych pochopil jak se to dělá
(nevím jestli to tam jde dobře vidět ale všechny zlomky tam jsou exponenty)
Offline
#2 10. 04. 2019 23:55
Re: složitější exponenciální rce
↑ Vojcek1339:
No, je to celkem zle napsané.
Nejdříve bych asi upravila výraz do příjemnější formy, tj. využila pravidla pro počítání s mocninami
a poté to řešila jako exp. rci.
Offline
#3 12. 04. 2019 22:08 — Editoval Vojcek1339 (12. 04. 2019 22:14) Příspěvek uživatele Vojcek1339 byl skryt uživatelem Vojcek1339.
#4 12. 04. 2019 22:28
- Vojcek1339

- Zelenáč
- Příspěvky: 13
- Reputace: 0
Re: složitější exponenciální rce
![kopírovat do textarea $[2\{2^{\sqrt{x}+3}\}^{\frac{1}{2\cdot \sqrt{x}}}]^{\frac{2}{\sqrt{x}-1}}=4$](/mathtex/ad/adccc5a1dca69a3b987dd2f4309ada93.gif)
sory udělal jsem tam chybu v prvním exponentu .. tady je správný výraz
Offline
#5 12. 04. 2019 22:48
#6 12. 04. 2019 23:27
- Vojcek1339

- Zelenáč
- Příspěvky: 13
- Reputace: 0
Re: složitější exponenciální rce
↑ laszky: dík ale mohl by jsi mi prosím napsat jak si přišel na to čím to umocnit protože já to asi nechápu
Offline
#7 12. 04. 2019 23:37
Re: složitější exponenciální rce
↑ Vojcek1339:
Podívej se na poslední exponent.
Co se stane, když to umocníš tím co napsal laszky?
Offline
#8 13. 04. 2019 00:05
Re: složitější exponenciální rce
↑ Vojcek1339:
Detailneji:
Vyraz v hranatych zavorkach na leve strane rovnice si upravis: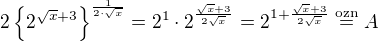
Rovnice ma tvar: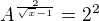
Umocnis-li ji na  prejde do podoby
prejde do podoby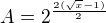 , neboli
, neboli
Offline
#9 13. 04. 2019 00:07
- Vojcek1339

- Zelenáč
- Příspěvky: 13
- Reputace: 0
Re: složitější exponenciální rce
↑ laszky: dík moc
Offline