Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 04. 2019 11:52 — Editoval stuart clark (18. 04. 2019 13:00)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
no. of real solution
If 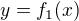 and
and  are two solution of the equation
are two solution of the equation 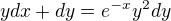
where 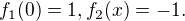 Then number of solution of
Then number of solution of 
Offline
#2 18. 04. 2019 13:01 — Editoval stuart clark (18. 04. 2019 13:02)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: no. of real solution
Thanks friends got it.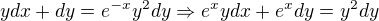
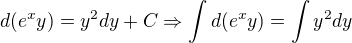
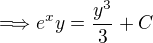
from condition, 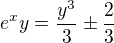
So  and
and 
So  and given
and given 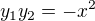
So 
Now drawing these two graph using derivative test, We have  real solution.
real solution.
Offline