Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Termodynamika I - Výpočet potřebného tepla dle rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 05. 2019 03:22
Termodynamika I - Výpočet potřebného tepla dle rovnice
Dobrý den.
Potřeboval bych, prosím, poradit s tímto příkladem, který si chci vypočítat z povinných příkladů cvičně na páteční zápočet z Fyziky. Bohužel jej zkrátka nemohu vypočítat, i když je na pohled velice lehký, ale obtížnost uvádějí až 3.
Poradíte mi, prosím? děkuji
Číslo příkladu: 435; Fyzika II, 9. přednáška; obtížnost: 3; pořadí: 54; počítá se ve cvičení; datum poslední změny:8.11.2007
Kolik tepla je zapotřebí, aby se látka, jejíž tepelná kapacita je dána rovnicí c = a + bt2, zahřála z teploty 0 °C na teplotu 20 °C? (a = 3, b = 4, t je ve oC a hmotnost látky jsou 2 kg. [Q = 21,5 kJ]
Výsledek je 21,5 kJ, co uvádějí v hranaté závorce na konci. Já to počítal takto, ale stejně mi to nevychází:
C = a + bt^2
C = 3 + 4 (20)^2
C = 1603 J.kg.K
Q = m * c * delta (t)
Q = 2 kg * 1603 J.kg.K * 20 °C
Q = 64 120 J = 64,12 kJ , což je úplně odlišný výsledek. Jelikož je to obtížnost 3, asi tam budou mnohem složitější kroky. Díky
Offline
- (téma jako vyřešené označil(a) DavidMath)
#2 08. 05. 2019 05:46
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
 není konstanta, takže ji nemůžeš vypočítat.
není konstanta, takže ji nemůžeš vypočítat.
K tomu, abys ohřál vodu z  na
na 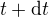 stupňů, potřebuješ
stupňů, potřebuješ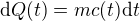 tepla.
tepla.
Kolik potřebujeme celkem tepla? Sečteme všechna elementární tepla: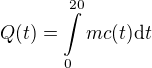
OK?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#3 08. 05. 2019 15:00 — Editoval DavidMath (08. 05. 2019 15:01)
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
Zmiňovaný integrál mi vyšel 200*m*c
po úpravách následujících: m*c* Integrál od 0 do 20 (t) dt = m*c* [(t^2/2)] od nuly do 20 = m*c* [(20^2/2) - (0^2/2)] = m*c* [(400/2) - 0] = 200m*c
Jenže nevím, jak postupovat dále... Za hmotnost dosadím 1 kg, to je jasné, ale co dosadím za to C?
Díky
Offline
#5 08. 05. 2019 15:14
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ MichalAld:
No, tak to je jedno, jestli to dosadím na začátku nebo až do výsledku ne? C je konstanta, neboť se jedná o násobek, takže stejně musí před integrál a tím pádem tohle C bude před závorkou až do výsledku. Takže bych teoreticky mohl dosadit za C do toho výsledku 200*m*c, to jsem zkoušel, ale nevychází to!
A jinak nerozumím, když bych měl dosadit ještě před počítáním integrálu, co by se na tom změnilo, respektive nevím, jak bych měl pak počítat... Omlouvám se
Offline
#6 08. 05. 2019 15:38 — Editoval DavidMath (08. 05. 2019 15:42)
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ MichalAld:
Jestli myslíte takto, tak mi to stejně nevychází, každopádně čísla výsledku jsou už totožná, akorát ve špatných řádech. Kde dělám chybu?
Omlouvám se za škrabopis, píšu to narychlo. Díky 
Edit: Aha, teď jsem si všimnul, že m není 1 kg jak jsem dosazoval, ale 2 kg, takže výsledek bude 2 * 2 133 393,33, což je blbost. Díky
Offline
#7 08. 05. 2019 15:56
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
Offline
#8 08. 05. 2019 15:59 Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Zbytečné
#9 08. 05. 2019 16:01 — Editoval DavidMath (08. 05. 2019 16:10)
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ pietro:
Nechápu ale, kam zmizelo to jedno t? Za integrálem má být přece m * c * t, takže by to mělo být m * (a + bt^2) [což je dosazené c] * zbývající t. Proč na Vašem odkaze tam to t není?
Protože tím pádem, když z mého výpočtu to t vyřadím (což po integraci je t^2/2, tak to těch 21 453 J vychází. Proč ale to t tam být nemá, když vzoreček integrace je jak uvádí viz výše ,,Kolega" KennyMcCormick ?
Offline
#10 08. 05. 2019 16:06 — Editoval DavidMath (08. 05. 2019 16:14)
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ Jj:
Ano, já tu integraci v podstatě mám v pořádku, akorát na začátku mám navíc jedno t, které po integraci je t^2/2, což pak samozřejmě násobek udělá mnohonásobně větší výsledek. Bez toho t je to poté správný výsledek.
Jen nerozumím, proč to t tam být nemá, protože nemá být náhodou Q = m*c*t nebo tento vzorec platí jen u kapacity C = m*c*t?
Edit: Takže Q = m*c , nikoliv Q = m*c*t. Zmátlo mě to, jak to poprvé uvedl uživatel KennyMcCormick, protože on psal do závorky t a já si myslel, že to je proměnná rovněž pro integraci, ale to (t) znamená jakože podle t.
Tím pádem mám tam to t na začátku navíc, a tím pádem mi to nevychází. Bez toho t to je v pořádku. Je to tak? :)
Jen pro C platí C = m*c*t a tady to t už je, neboť je to vzorec se změnou teploty. :)
Offline
#11 08. 05. 2019 16:11
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ DavidMath:
Kolega nepíše m*c*t, ale m*c(t), tzn., že c je funkcí t.
Pokud se tedy nemýlím.
Offline
#12 08. 05. 2019 16:13
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ Jj:
Ano ano, všimnul jsem si toho, viz můj edit nahoře červeně. Blbě jsem si to napsal, a pak už jsem s tím t rovněž počítal, což je špatně. Děkuji mnohokrát ;)
Offline
#13 08. 05. 2019 16:19 — Editoval Jj (08. 05. 2019 16:25)
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ DavidMath:
A ještě k té integraci, kdyby tam to t patřilo, tak by byla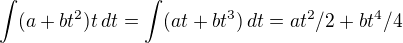
Takže nelze souhlasit s tímto:
"Ano, já tu integraci v podstatě mám v pořádku, ... "
Pokud se tedy nemýlím.
Offline
#14 08. 05. 2019 17:58 — Editoval MichalAld (08. 05. 2019 18:00)
Re: Termodynamika I - Výpočet potřebného tepla dle rovnice
↑ DavidMath:
Ono je to buď takto (to platí vždycky)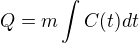
nebo (v případě, že C je konstantna, a nezávisí na teplotě, tedy že C(t) = C) takto: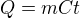 nebo tedy správně by to mělo být
nebo tedy správně by to mělo být 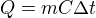 , protože jde o rozdíl teplot, né o absolutní teplotu.
, protože jde o rozdíl teplot, né o absolutní teplotu.
Nikdy to ovšem není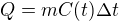 (tohle by mohlo být ještě zhruba správně, kdyby ten rozdíl teplot byl malý)
(tohle by mohlo být ještě zhruba správně, kdyby ten rozdíl teplot byl malý)
a už vůbec né
či 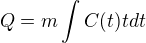
Offline
#15 09. 05. 2019 03:19
Stránky: 1
- Hlavní strana
- » Fyzika
- » Termodynamika I - Výpočet potřebného tepla dle rovnice (TOTO TÉMA JE VYŘEŠENÉ)

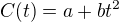 , ale ještě před tím, než začneš počítat ten integrál...
, ale ještě před tím, než začneš počítat ten integrál...