Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 05. 2019 11:22
lokální extrémy
Dobrý den, mám tu jeden příklad na lokální extrémy, při kterém mi D2 vychází záporně tudíž by neměl ten lokální extrém, jen si nejsem jistej jestli počítám správně, kdyby na to někdo mohl kouknout:
1. derivace podle x: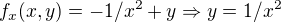
1. derivace podle y:
Vyjádřený y jsem si dosadil do druhé rovnice abych našel stacionární body: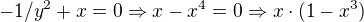
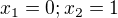
Pro  není bod
není bod  protože nelze dělit nulou.
protože nelze dělit nulou.
Pro  platí:
platí: 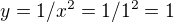
Takže stacionární bod by byl ![kopírovat do textarea $A=[1,1]$](/mathtex/f5/f5383532381cc0073897a693ab481185.gif)
Druhé derivace: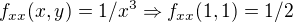
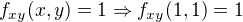
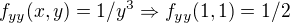

To  jsem počítal klasicky jako determinant, akorát nevím jak sem můžu vložit matici tak jsem nerozepisoval.
jsem počítal klasicky jako determinant, akorát nevím jak sem můžu vložit matici tak jsem nerozepisoval.
Za případné opravy a případnou pomoc předem děkuji.
Offline
- (téma jako vyřešené označil(a) byk7)