Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 23. 05. 2019 17:13 — Editoval krakonoš (23. 05. 2019 17:18)
Re: Konvergence řady
↑ m.sey:
Ahoj.Zvolme n sude.Vynaspb to a vyděl zaroveň výrazem (1 plus cos(1/2n)
Pak dostanes sinus,to se na okoli nuly chova jako argument.V tomto pripade jako 1/2n krat 1/2n . Druha mocnina n jde ale v nekonecnu mnohem pomaleji nez 2n na 4n.
Takze to nevidim na tu nulovou limitu.
Pro n liche by to melo byt podobne.Zrejme to vede k minus nekonecnu,limita nebude existovat.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline

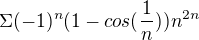 , rád bych to typově řešil podle Leibnitzova krit., ale nevím jak zjistit aby
, rád bych to typově řešil podle Leibnitzova krit., ale nevím jak zjistit aby 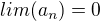 . V limitě jsem získal jen
. V limitě jsem získal jen 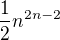 . Poradíte?
. Poradíte?