Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 05. 2019 02:44
Re: nested summation with integration
↑ stuart clark:
Hi.
Is the first integral definite or indefinite?
Is  a parameter, or is it just a missprint?
a parameter, or is it just a missprint?
For the first integral I found, that since there holds ,
,
we have 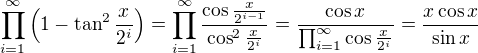
and hence
Offline
#3 25. 05. 2019 11:13
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: nested summation with integration
Thanks Laszky actually it is given by someone to me and i also seems that it is wrong.
Offline
![kopírovat do textarea $\int \frac{1}{x}\prod^{\infty}_{i=1}\bigg(1-\tan^2 \frac{x}{2^i}\bigg)dx\cdot \frac{1}{\ln\bigg(\sum^{\infty}_{\alpha =1}\bigg[\int^{\infty}_{0}\frac{x^{\alpha-1}\cdot e^{-\frac{1}{n}}}{n\cdot ((\alpha-1)!)^2}dx\bigg]\bigg)}$](/mathtex/27/275e67740b22261c04d9b6a1a75e1949.gif)