Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Chemie
- » Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
#1 25. 05. 2019 22:50 — Editoval DavidMath (25. 05. 2019 22:51)
Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
Dobrý den.
Prosím Vás, nevím si vůbec rady s tímto příkladem.
Přijde mi ten postup celkem běžný, spíše je horší dát dohromady celkový vzoreček, který je tam spojený nějak dohromady a vůbec se v tom nemohu zorientovat.
Co vím, tak výpočet obsahu analytu ve vzorku (co se týče pevného vzorku v roztoku) je dle mě dle vzorečku:
ma = a/b * Ma * Cs * Vs * fa , kdy fa je podílový (gravimetrický) faktor objem vzorku dělený pipetovaným objemem vzorku.

Proto absolutně nechápu řešení příkladu, které je sice naštěstí v materiálech ke zkoušce uvedeno, to ovšem neznamená, že mi to nějak pomůže, dokud nepochopím samotný princip a co se tam vlastně odehrává co se týče výpočtu.
Jelikož je to spíše zobecnění vzorečků, protože je tam zakomponována Normalita, která už vypadá zase úplně jinak (N = m/E * A), kdy E je ekvivalentová molární hmotnost. Normalita je asi i N = η/V), popravdě i celkově tady těmto vzorečkům v této obecné podobě v podobě spíše hodně nepředstavitelných entit a ekvivalentů moc rozumět neumím, ale pořád to ještě jde.
Vůbec tedy nechápu, proč je konečný vzoreček viz druhý snímek v podobě:
m = M/(b * 1000) * A * N * podílový faktor
m(CaO) = 56,077/(2 * 1000) * 33,3 * 0,1234 * 1000/25 = 4,6087 g/l.
To je sice moc krásné :D, ale já se v tom úplně ztrácím.
Zaprvé, proč je molekulová hmotnost CaO v čitateli a je dělená násobkem stechiometrického koeficientu s celkovým objemem vzorku (1000 ml), dále to je v podstatě alespoň trochu podobné tomu, co jsem psal, tedy vzorečku pro výpočet obsahu analytu ve vzorku (pevný vzorek v roztoku), protože 33,3 je počet spotřebovaného odměrného činidla, 0,1234 je normalita (tedy asi tedy koncentrace toho odměrného roztoku ?), a ten podíl 1000/25 je ten podílový faktor (celkový objem dělený pipetovaným objemem vzorku).
Jako celek to ale nechápu, když porovnám běžný vzoreček pro výpočet obsahu analytu pevného vzorku v roztoku s tímto vzorečkem, prostě mi to nedává smysl a vůbec by mě to takto nenapadlo. Navíc už to, že Molekulová hmotnost je nahoře a je dělená násobkem 2 * 1000.
A jak vůbec poznám, jaký objem kam přijde? Proč nepůjde třeba objem spotřeby 33,3 do jmenovatele místo celkového objemu 1000 ?
Mohli byste mi, prosím, poradit?
děkuji moc!
Offline
#2 25. 05. 2019 23:55 — Editoval Bedlasky (25. 05. 2019 23:55)
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
↑ DavidMath:
Zdravím.
No, upřímně - nikdy jsem neměl rád tyhle různé analytické faktory a já nevím co - také jsem se v tom ztrácel. Nemluvě o tom, že jsem líný si věci pamatovat, tak si je radši odvozuju (nebo když je jo často používám, tak si je někam napíšu). Nevím, jak moc to po Vás vyžadují si to pamatovat.
Z rovnice vyplývá že: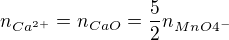
A teď už jen za látková množství dosadit co je potřeba.
n = c×V
n = m/M
V případě že ředíte tak: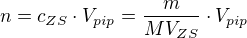
Kde 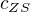 je koncentrace zásobní roztoku,
je koncentrace zásobní roztoku, 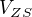 je objem zásobního roztoku,
je objem zásobního roztoku, 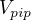 je kolik jste ze zásobního roztoku odpipetoval, m je hmotnost rozpuštěné látky, M je molární hmotnost rozpuštěné látky
je kolik jste ze zásobního roztoku odpipetoval, m je hmotnost rozpuštěné látky, M je molární hmotnost rozpuštěné látky
Offline
#3 26. 05. 2019 01:17
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
Děkuji za odpověď, každopádně tomu pořád nerozumím.
Vy jste napsal, že:
Bedlasky napsal(a):
V případě že ředíte tak:
Kdeje koncentrace zásobní roztoku,
je objem zásobního roztoku,
je kolik jste ze zásobního roztoku odpipetoval, m je hmotnost rozpuštěné látky, M je molární hmotnost rozpuštěné látky
Jenže pořád to není podobné tvaru, který jsem napsal.
Přece když je c = m/M*V, tak vyjádření m = c * M * V, proto nechápu, že ve vzorci, který jsem uváděl, je m vyjádřeno úplně zvláštně, navíc jak se molekulová hmotnost dostala do čitatele?
Celkově to totálně nechápu :D. Taky nechápu, proč ve vzorci jsou v podstatě uvedeny až tři objemy - jak mám tedy poznat, který objem patří kam? Jeden objem je spotřeba činidla = 33,3, druhý objem je v podstatě celý podílový faktor (tedy podíl celkového a pipetovaného objemu) a třetí objem je celkový objem ve jmenovateli násobený stechiometrickým koeficientem.
Rád bych to alespoň pomocí nějakého vysvětlení, případně opět, bohužel, podorbějšího rozepsání, pochopil.
Děkuji Vám i všem ostatním za případnou pomoc ;)
Offline
#4 26. 05. 2019 15:11
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
↑ DavidMath:
Tak budeme dosazovat sem: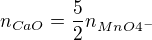
Vody jste si bral 25ml z 1 litru, takže na to se použije to třetí (chcete vědět množství CaO v celém litru, ne jen v těch 25ml). No a na manganganistan se použije ten první, to Vám udává kolik molů jste ho spotřeboval.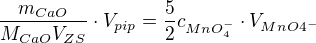
Vyjádřete si hmotnost CaO a dostane výsledek.
Offline
#5 26. 05. 2019 18:55
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
↑ Bedlasky:
Všichni se shodujeme na tom, že n(CaO) = (5/2)*n(MnO4-) . Dále
c(CaO) = n(CaO)/0,025 = (5/2)*n(MnO4-)/0,025 [mol/dm3] a konečně
cm(CaO) = c(CaO)*M(CaO) = 56,077*2,5*n(MnO4-)/0,025 [g/dm3]
OK?
Offline
#7 23. 06. 2019 14:07
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
↑ Jozka2:
Bohužel dle obou postupů to stále vychází špatně, a to 23,04 g/l ....
má to vyjít viz zadání. Popravdě, tady si vůbec nevím rady jakýmkoliv postupem jiným, lepším a přehlednějším, než jaký je v zadání a výsledku počítání v materiálech.
:( Mohl by mi prosím někdo poradit?
Offline
#8 23. 06. 2019 18:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
Zdravím,
↑ DavidMath: podle reakce v úplně úvodním příspěvku, kde 5H2C2O4+2MnO4(-)... platí, co píšou kolegové ↑ Bedlasky: a ↑ Jozka2:, že
n(CaO) = (5/2)*n(MnO4-)
ovšem ve vzorci pro m(CaO) není zohledněno (5/2). Co označujete písmenem  ve vzorci pro
ve vzorci pro  ?
?
Jinak také, jak píšou kolegové, bych postupovala odvozením - já tedy podle trojčlenek. Hotový vzorec tohoto typu snad má smysl, když máš přímo hotový metodický návod, nebo pro "automatický" výpočet, že data vložiš do některého kalkulátoru se zabudovaným vzorcem. Upřesní, prosím, co je  . Děkuji.
. Děkuji.
Offline
#9 25. 06. 2019 13:55
Re: Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
↑ DavidMath: a ↑ Bedlasky:
Sice jsem to nepočítal, ale není náhodou problém v tom, že Pořád uvažujete s c(MnO4-) = 0,1234M, zatím co v zadání je 0,1234N - normální, ne molární. Normalita KMnO4 je 5x menší než jeho molarita:
0,1M KMnO4 = 0,5N KMnO4!
Offline
Stránky: 1
- Hlavní strana
- » Chemie
- » Výpočet obsahu analytu - normalita, ekvivalentová molární hmotnost...
