Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Parciální diferenciální rovnice - heat equation
#1 27. 05. 2019 10:15
Parciální diferenciální rovnice - heat equation
Prosím o vysvětlení, krok za krokem, jak dostanu, že řešením následující parciální diferenciální rovnice
je zrovna
Chápu, že hledám funkci, která to splňuje a že jich je mnoho..jenže si neumím poradit, jak z toho předpisu mám dostat tu funkci.
Děkuji
Offline
#2 27. 05. 2019 10:58 — Editoval jarrro (27. 05. 2019 11:05)
Re: Parciální diferenciální rovnice - heat equation
Záleží v akom tvare chceš riešenie ak to má byť v tvare ,
,
tak dosadením do rovnice zistíš, že 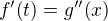
Čo je zrejme možné len keď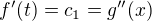
Teda
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Parciální diferenciální rovnice - heat equation

