Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2019 01:35 — Editoval Ikaruss (29. 05. 2019 01:37)
Goniometrie -příklad
Zdravím, mám tenhle příklad a netuším, jak se tento typ počítá:
Jestliže cotgα=−1, pak cos2α se rovná číslu?
Já vím, že tady je ve zvyku spíš napovědět, ale ocenil bych, pokud by mi postup počítání někdo rozepsal, moc by mi to pomohlo. Díky:)
Offline
#3 30. 05. 2019 13:46 — Editoval vojta.tlustý (30. 05. 2019 13:49)
- vojta.tlustý

- Zelenáč
- Příspěvky: 24
- Škola: Gymnázium Františka Marina Pelcla v RK
- Pozice: student
- Reputace: 1
Re: Goniometrie -příklad
Stačí si uvědomit, jaku už bylo uvedeno výše že Cotg α je vlastně sinα/cosα poté se stačí podívat do grafu, kdy se funkce sinus a cosinus protnou, tedy kdy mají stejnou hodnotu. To nastává v 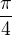 a
a 
Poté si zaneseš hodnoty do jednotkové kružnice a pootočíš s nimi o 90 stupňů tak, aby obě hodnoty ležely v takovém kvadrantu ve kterém je jedna funkce záporná a druhá kladná, tedy do 2. a do 4. tedy  a
a 
Nyní jsme získaly hodnotu  můžeme napsat
můžeme napsat 
na poslední člen nesmíme zapomínat, neboť bez něj by nám mohlo zmizet jedno, nebo i více řešení. Tohle není ten případ, ale vyplatí se to dělat vždy, lepší to dělat vždy, než na to u těžších příkladů zapomenout.
V tuto chvíli stačí jen dosadit za α, dostaneme  na jednotkové kružnici leží
na jednotkové kružnici leží 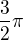 přímo pod
přímo pod  takže výsledek bude jedna velká nula.
takže výsledek bude jedna velká nula.
Offline
#4 30. 05. 2019 21:56
Re: Goniometrie -příklad
↑ vojta.tlustý:
Zdravím,
vojta.tlustý napsal(a):
Stačí si uvědomit, jaku už bylo uvedeno výše že Cotg α je vlastně sinα/cosα
To není ani uvedeno v příspěvku ↑ byk7:, ani to není pravda. Jak píše kolega ↑ byk7:, 
Offline
 .
. a
a  ?
? ?
? spočítat úhel
spočítat úhel  a pak přímo dosadit.
a pak přímo dosadit.
