Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spočtěte integrál pomocí integrálu v komplexní proměnné
#1 05. 06. 2019 11:54
- dominiksep
- Příspěvky: 54
- Reputace: 0
Spočtěte integrál pomocí integrálu v komplexní proměnné
Ahoj,
už poněkolikátý počítám následující příklad a nemůžu zjistit, kde mám chybu:
Pomocí integrálu v komplexní proměnné spočtěte
Provedu substituci 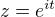 , čímž mi vznikne integrál
, čímž mi vznikne integrál
pro křivku ![kopírovat do textarea $\varphi = e^{it}, \; i \in [0;2\pi]$](/mathtex/6b/6be7ffe81a4303f14e1b589508552720.gif)
Výraz ve jmenovateli má dva kořeny 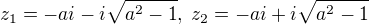 .
.
Lze ukázat, že první kořen leží mimo křivku, první leží uvnitř pro všechna uvažovaná  .
.
Spočtu tedy integrál pomocí reziduové věty. Máme pól 1. řádu, vzorec pro výpočet se tedy zjednoduší na 
V reziduové větě pak
Problém však nastává, když si tento integrál hodím do Wolframu - vyjde jiný výsledek.
asi tam bude nějaká numerická chyba, ale já už ji fakt nevidím...
Díky
Offline
#2 05. 06. 2019 14:23 Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Zřejmě omyl.
#3 05. 06. 2019 21:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spočtěte integrál pomocí integrálu v komplexní proměnné
Zdravím,
nejdřív je potřeba trochu "učesat": pokud byl použit Euler. vzorec a následná substituce 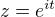 , potom pro křivku není
, potom pro křivku není ![kopírovat do textarea $i \in [0;2\pi]$](/mathtex/97/972b301eef7ca10b1636ee7ab39a9597.gif) , ale
, ale ![kopírovat do textarea $t \in [0;2\pi]$](/mathtex/ac/ac7f3fd9d87391a591b1f9a216d54917.gif) . Dál v zápisu
. Dál v zápisu  chybí
chybí 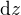 , tedy
, tedy  .
.
A nakonec pro pol 1. řádu platí 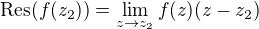 - souhlasí? A tedy v čitateli
- souhlasí? A tedy v čitateli
nemá být  , jen
, jen 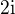 .
.
Souhlasí to? Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spočtěte integrál pomocí integrálu v komplexní proměnné

