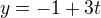Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 31. 05. 2009 09:20 — Editoval adamo (31. 05. 2009 09:45)
Re: Rovnice tečny ke kružnici
1) Vypiš si směrový vektor (2,3) převeď jej na normálový vektor, např. (3,-2) a sestav obecnou rovnici přímky s parametrem c. Normálně bys potřebovala dosadit ještě bod ležící na přímce, abys zjistila parametr c, ale ten je ti v tomto případě na nic, protože hledáš rovnoběžku. Mě vyšlo: 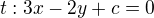
2) z této rovnice si vyjádři libovolnou proměnnou, já volím x: 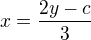
3) dosadíš do rovnice kružnice a poupravuješ. Vyšla mi kvadratická: 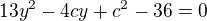
4) vypočítáš diskriminant a položíš roven nule, protože pokud je D=0 pak bude ta přímka mít pouze jeden společný bod: 
No takže výsledné tečny jsou:
Doufám že jsem neudělal chybu, jsou to docela netradiční čísla... Každopádně po nakreslení to vyšlo...
Offline
#6 31. 05. 2009 13:28
- marnes

- Příspěvky: 11227
Re: Rovnice tečny ke kružnici
↑ leniczcha:
1) K té obecné rovnici. Je takové nepsané pravidlo - nebo je lepší psát- +c do obecné rovnice. Proč? V tomto příkladě to bylo jedno, protože ti vyšly kořeny opačná čísla. Kdyby ti ale vyšlo číslo třeba -4 a 5, tak ty by jsi si musela dát pozor při psaní rovnice na to mínus před c a musela by jis dosadit -(-4) a -5. Zatímco když tam budeš mít v obecné rovnici plus c, tak jen dosadíš čísla, která ti vyšla
2) K té parametrické rovnici. Určitě, ale je to zbytečné. Napíšu k t1. Z obecné rovnice vyčtu normálový vektor (3;-2) a napíšu směrový, potřebný k PR u=(2;3)
x= Xa+2t
y= Ya+3t t patří R Ještě potřebuješ bod, kterým přímka prochází A=[Xa;Ya] nejlépe je si za Xa zvolit nulu Xa=0 a dosazením do OR vypočítat Ya. Pro náš případ vyjde Ya=odm(52)/2=odm(13)
x= 2t
y= odm(13)+3t t patří R
Jo. A na začátku vás zdravím.
Offline
#8 31. 05. 2009 13:42 — Editoval marnes (31. 05. 2009 13:43)
- marnes

- Příspěvky: 11227
Re: Rovnice tečny ke kružnici
↑ leniczcha: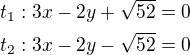 Jestli se bavíme o těchto rovnicích, tak to určitě ne. Už jen směrový vektor je špatně
Jestli se bavíme o těchto rovnicích, tak to určitě ne. Už jen směrový vektor je špatně
Jo. A na začátku vás zdravím.
Offline
#9 31. 05. 2009 13:48
Re: Rovnice tečny ke kružnici
Takže v tomto případě jsou tyto rovnice špatně, protože výsledek k zadání:
Napište rovnici tečny ke kružnici, která je rovnoběžná s danou přímkou:
x^2 + y^2 = 4
x = 2 + 4t
y = 3 + 3t
Výsledek:
x = 2 + 4t
y = 4 + 3t
a
x = 2 + 4t
y = -1 + 3t
Offline
#10 31. 05. 2009 14:05
- marnes

- Příspěvky: 11227
Re: Rovnice tečny ke kružnici
↑ leniczcha:Ano, pak jsou rovnice špatně, protože směrový vektor musí být stejný, tj (4;3) Obecné rovnice tečen musí začínat 3x-4y+c=0
Jo. A na začátku vás zdravím.
Offline
#12 04. 02. 2015 09:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tečny ke kružnici
↑ Lucas89:
Zdravím,
pokud je dotaz k původní úloze
Napište rovnici tečny ke kružnici, která je rovnoběžná s danou přímkou:
x^2 + y^2 = 4
x = 2 + 4t
y = 3 + 3t
potom pomocí D jsi měl dojit k souřadnicím bodů doteku (jsou na kružnici, kružnice má s tečnou jeden společný bod, ovšem takových tečen rovnoběžných se zadanou přímkou může být 2 - pokud sama přímka již není tečnou, potom + další jedna). Rovnoběžné přímky mají stejný směrový vektor se zadanou přímkou. To se objeví ve směrovém vektoru nových přímek:
x = 2 + 4t
y = 4 + 3t
a
x = 2 + 4t
y = -1 + 3t
V tématu se ale diskutuje, že něco je chybně v postupu, nebo neshoda s výsledky (?), tak snad ještě projít celý postup od začátku.
Offline

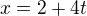 ,
, 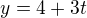 nebo
nebo