Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Odvození tenzoru napětí u viskózních kapalin
#1 07. 07. 2019 16:22
- vojtechremis

- Zelenáč
- Příspěvky: 3
- Reputace: 0
Odvození tenzoru napětí u viskózních kapalin
Zdravím,
zajímalo by mě, kde se vzal tenzor napětí u viskózních kapalin. Prosím o konkrétní odvození, abych tomuto problému mohl opravdu rozumět.
Předem děkuji za jakoukoliv radu a přeji hezký den.
Offline
#2 07. 07. 2019 22:55
Re: Odvození tenzoru napětí u viskózních kapalin
Ahoj,
dana forma tenzoru napeti je jen jeden z moznych modelu tekutin. Zde konkretne jde o nestlacitelnou Newtonovskou tekutinu. Pro jine tekutiny nebude tento model odpovidat realite. Proto je treba ten vztah vnimat spis jen jako predpoklad. Pak ale je otazka, proc se pouziva zrovna tenhle predpoklad. Zde jsou duvody:
- tenzor napeti by obecne mel zaviset na gradientu rychlosti, ostatni zavislosti jsou zanedbany
- tekutina je nestlacitelna, tzn. stopa gradientu rychlosti je vzdy nula, takze o stope tenzoru napeti nemame zadnou informaci, proto se pricita -pI, kde p je neznama, ktere se rika tlak
- ve skutecnosti tenzor napeti nemuze zaviset na gradientu rychlosti ale jen na jeho symetricke casti kvuli konzistenci teto zavislosti pri zmene pozorovatele
- chceme aby vztah byl konzistentni s Newtonovym experimentem, tj. ze v jednoduchem smykovem proudeni by mela smykova sila byt primo umerna rozdilu rychlosti
- vyssi mocniny gradientu rychlosti jsou zanedbany, nebot ty vedou na modely pro nenewtonovske tekutiny
Z toho uz vychazi vztah, co jsi napsal
Offline
#3 09. 07. 2019 18:44
- vojtechremis

- Zelenáč
- Příspěvky: 3
- Reputace: 0
Re: Odvození tenzoru napětí u viskózních kapalin
↑ Bati:
Moc Vám děkuji za odpověď. Mohl byste prosím rozvést to, proč je tenzor symetrický?
Rozumím tomu, že to musí korespondovat s Newtonovým zákonem viskozity, ale stále bych na základě těchto informací neuměl takový tenzor odvodit (tu část s vnitřním třením). Konkrétně ty součty parciálních derivací a pak proč u těch normálových napětí je dvojnásobek gradientu. Viděl jsem, že to má nějakou souvislost s tenzorem malých deformací, ale moc to nechápu.
Předem děkuji za odpověď.
Offline
#4 12. 07. 2019 01:14
Re: Odvození tenzoru napětí u viskózních kapalin
Ty soucty parcialnich derivaci presne odpovidaji symetricke casti gradientu: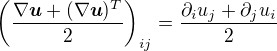 .
.
To jaky nasobek te matice tam je zavisi na tom, cemu budeme rikat viskozita. Pokud je to to mi, pak to ma tu vyhodu, ze divergence tenzoru napeti vyje  .
.
To, ze tenzor napeti musi zaviset jen na symetricke casti gradientu plyne z tzv. principu objektivity: Mejme 2 pozorovatele - kazdy pouziva pro popis te same tekutiny svuj souradny system. Predpokladejme ze druhy system je jen nejaka casove zavisla rotace toho prvniho, tj. je-li  bod v prvnim systemu, ten samy bod ve druhem systemu je
bod v prvnim systemu, ten samy bod ve druhem systemu je 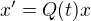 , kde
, kde 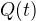 je matice rotace (unitarni). Oznacme
je matice rotace (unitarni). Oznacme  vztah mezi tenzorem napeti a symetrickym gradientem rychlosti. Prvni pozorovatel vidi, ze
vztah mezi tenzorem napeti a symetrickym gradientem rychlosti. Prvni pozorovatel vidi, ze 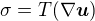 a druhy vidi
a druhy vidi 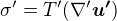 . Protoze chceme aby fyzikalni zakony platily pro oba pozorovatele stejne, musi byt
. Protoze chceme aby fyzikalni zakony platily pro oba pozorovatele stejne, musi byt  . Pak ale
. Pak ale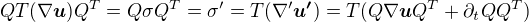 (over si)
(over si)
To je nesplnitelne pokud  neni konstantni v case. Naproti tomu, se symetrickym gradientem to vyjde
neni konstantni v case. Naproti tomu, se symetrickym gradientem to vyjde
coz naopak je automaticky splneno napr. pro zmineny linearni vztah (Newtonovska kapalina).
Offline
#5 29. 07. 2019 09:20
- vojtechremis

- Zelenáč
- Příspěvky: 3
- Reputace: 0
Re: Odvození tenzoru napětí u viskózních kapalin
↑ Bati:
Děkuji Vám moc za pomoc :)).
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Odvození tenzoru napětí u viskózních kapalin