Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » "párny integrál" (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 08. 2019 11:14 — Editoval jarrro (08. 02. 2023 06:52)
"párny integrál"
Čaute mám tu (aspoň pre mňa)zaujímavú úlohu. Nech
[mathjax]
\begin{align}\mathbb{R}\ni a>0, \mathbb{R}\ni b>0\\
f:\left(-a,a\right)\to\mathbb{R} \text{ je párna}\\
g:\left(-a,a\right)\to\mathbb{R} \text{ je nepárna}\\
\int\limits_{0}^{a}{f{\left(x\right)}\mathrm{d}x}=I\in\mathbb{R}^{*}\end{align}[/mathjax]
Určte
[mathjax]\int\limits_{-a}^{a}{\frac{f{\left(x\right)}}{1+b^{^{^{g{\left(x\right)}}}}}\mathrm{d}x}[/mathjax]
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 14. 08. 2019 12:19
#3 14. 08. 2019 13:44 — Editoval jarrro (14. 08. 2019 13:47)
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » "párny integrál" (TOTO TÉMA JE VYŘEŠENÉ)

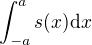 , kde
, kde 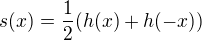 a
a 
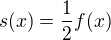 , a proto
, a proto  ?
?