Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 05. 2009 07:37 — Editoval drsnak (31. 05. 2009 07:37)
kvadraticke reovnice



prosil bych o vypocitani techto rovnic a jestli by bylo mozne jestli byste je rozepsali trochu vic nas pan ucitel nam to moc nevysvetlil a ja bych se to rad nauci predem dekuji! a preji prijemny den
(prominte ze vas s tim otravuji)
Offline
#2 31. 05. 2009 09:34
Re: kvadraticke reovnice
v každé rovnici převeď vše na levou stranu, aby se pravá rovnala nule, pak vypočítej diskriminant podle vzorce 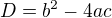 , potom řešení
, potom řešení 
kde a je koeficient kvadratického členu, třeba pro 3x^2 je to 3, b je koeficient lineárního členu, pro 2x je to 2, a c je absolutní člen, třeba 5,
z rovnice 4c^2-c+2=0 bude a=4,b=-1,c=2. teď už to snad zvládneš.
R. P. Feynman:Fyzika je jako sex, může přinést praktické výsledky, ale to není důvod, proč to děláme.
Offline
#7 31. 05. 2009 22:40
Re: kvadraticke reovnice
↑ halogan:dekuju moc hodne mi to pomohlo zkusim ty dalsi sam ale jeste se musim zeptat bylo by taky mozny kdyby x2=3/5 a x1=-2
Offline
#8 31. 05. 2009 22:42
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: kvadraticke reovnice
↑ drsnak:
Samozřejmě. Ty kořeny nejsou nijak řazeny. Jedině kdybys hledal kořen graficky, tak se zpravidla čísluje ten nižší (tedy -2 v tomto případě) jako x_1 a ten druhý jako x_2, ale není to podstatné.
Offline
#9 31. 05. 2009 22:43
Re: kvadraticke reovnice
↑ halogan:jo A jeste bych se rad zeptal jestli si ten vysledek muzu overit zkouskou ( jak se dela zkouska u kvadratickejch rovnic!!!
Offline
#10 31. 05. 2009 22:45
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: kvadraticke reovnice
↑ drsnak:
Klasickým dosazením. Správně uvažuješ, že chceš provést zkoušku.
Na levé straně by ti měla vyjít nula, čímž pádem vyjde 0 = 0.
Jinak když máš ty kořeny, tak se dá daná rovnice zapsat jako 
V tomto případě 
A po roznásobení by měl vyjít opět původní předpis.
Offline
#13 31. 05. 2009 23:07
Re: kvadraticke reovnice
↑ halogan: jeste se musim zeptat co si myslel tim ze na leve strani by mela vyhit 0 0=0
prosimte jak mam udelat zkousku aby mi na leve strani vysla 0??
Offline
#14 31. 05. 2009 23:14
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: kvadraticke reovnice
Mějme původní rovnici:
Vyšly nám dva kořeny: -2 a 3/5. Jsou to kořeny, protože splňují tu rovnici, po jejich dosazení se opravdu levá strana rovná nule.
Jak si to ověříme? Dosadíme:
Za x budu dosazovat nejprve -2, vyjde mi:
5*4 - 14 - 6 = 0, což platí, protože 20 - 14 - 6 je nula.
Teď to samé s 3/5:
5*(9/25) + 21/5 - 6 = 0
45/25 + 21/5 - 6 = 0
9/5 + 21/5 - 6 = 0
30/5 - 6 = 0
0 = 0
Což také platí.
Oba kořeny jsme tedy ověřili zkouškou.
Offline
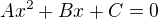 , spočítej si diskriminant
, spočítej si diskriminant  , který odmocníš a pak vypočítáš kořeny následovně:
, který odmocníš a pak vypočítáš kořeny následovně:





