Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 18 19 20 21 22 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#476 10. 09. 2019 16:56 — Editoval vanok (11. 09. 2019 22:23)
Re: Limitny maraton
Ahoj ↑↑ vanusok:,
Mozes si pozriet #479.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#477 10. 09. 2019 18:12
#478 10. 09. 2019 22:06 — Editoval vanok (10. 09. 2019 23:37) Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Zbytocne
#479 10. 09. 2019 23:00 — Editoval vanok (11. 09. 2019 22:29)
Re: Limitny maraton
Tu dam jednu cestu k moznemu rieseniu problemu (91) ( i ked som vyssie dal dostatocne indikacie na jeho riesenie).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#480 10. 09. 2019 23:13 — Editoval krakonoš (10. 09. 2019 23:34) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#481 10. 09. 2019 23:33 Příspěvek uživatele vanok byl skryt uživatelem vanok.
#482 11. 09. 2019 07:31 Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#483 11. 09. 2019 07:48
#484 11. 09. 2019 08:01 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Zbytocne
#485 11. 09. 2019 09:58 — Editoval krakonoš (11. 09. 2019 10:48) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#486 11. 09. 2019 11:46 — Editoval vanok (11. 09. 2019 13:42) Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Zbytocne
#487 11. 09. 2019 12:13 — Editoval krakonoš (11. 09. 2019 12:42) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#488 11. 09. 2019 13:41 — Editoval vanok (11. 09. 2019 14:40) Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Zbytocne
#489 11. 09. 2019 22:26
Re: Limitny maraton
Pozdravujem,
Pre kontrolu som ukazal jednu cestu k reseniu problemu (91) v #479.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#490 13. 09. 2019 17:09
#491 13. 09. 2019 21:56 — Editoval krakonoš (13. 09. 2019 22:00)
Re: Limitny maraton
↑ jardofpr:
Ahoj.
Tento příklad jsem našla mezi nevyřešenými ve fóru.
V okolí nuly jsem uvažovala podobně jako ty. V okolí nekonečna ( interval K,nekonečno. ) mi připadá použitelnéDirichletovo kriterium pro konvergenci integrálů t.j. omezená primitivní funkce k sinx, počínaje nějakým x rovno K bude funkce log(x plus1)/xnadruhou klesající a mít nulovou limitu....atd.
Tvůj postup je rychlejší,stačí si na závěr uvědomit per partes.
Díky.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#492 14. 09. 2019 08:49 — Editoval Bati (14. 09. 2019 08:50)
Re: Limitny maraton
↑ krakonoš:
Ahoj. Poznamka: logaritmus neni potreba integrovat, vime, ze  je v okolí nekonečna klesající pro libovolné
je v okolí nekonečna klesající pro libovolné  a ze
a ze  konverguje pro
konverguje pro  . Jinymi slovy, potreba integrovat by byla az v hranicnim pripade
. Jinymi slovy, potreba integrovat by byla az v hranicnim pripade  , ktery s prehledem majorizuje ten zadany.
, ktery s prehledem majorizuje ten zadany.
Offline
#493 14. 09. 2019 10:26 — Editoval krakonoš (14. 09. 2019 10:31)
Re: Limitny maraton
↑ Bati:
Ahoj
Máš pravdu.To by stačilo,protože je N integrál brán vždy na otevřeném intervalu.
Co se týče pravého okolí nuly resp. mezí integrálu 0,K.,uvažovala jsem podobně jako jardofpr, jedině s tím rozdílem,že v nule lze zadanou funkci spojitě dodefinovat.Pak můžu uvažovat o spojité funkci., která je na uzavřeném intervalu vždy shora i zdola omezená konstantní funkcí a dale lze tedy vytvorit konvergentní majoritní integrál .
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#494 14. 09. 2019 11:38 — Editoval vanok (14. 09. 2019 11:39)
Re: Limitny maraton
Problem (93).
Vysetrite konvergenciu ![kopírovat do textarea $\int_{1}^{+\infty}\frac {dx}{x^{[x]}}$](/mathtex/7a/7a0b75990723c52530b3f771fff748b1.gif) , kde
, kde ![kopírovat do textarea $[x]$](/mathtex/21/21271f70d45cc2a593fb2a4b47a16998.gif) je cela cast z
je cela cast z  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#495 15. 09. 2019 14:59
Re: Limitny maraton
Offline
#496 15. 09. 2019 16:46 — Editoval krakonoš (15. 09. 2019 16:54)
Re: Limitny maraton
↑ jardofpr:
Ahoj.
Já použila podobný postup.Jedině jsem osamostatnila první člen (ln2), pak si spočetla integrál,vytkla společný zlomek, který je vždy roven nebo menší než 1 (pro horni odhad) a u rozdílu primitivních funkcí menšitele položila rovného nule (horní odhad).Dostala jse tedy tutéž výslednou řadu jako ty,tu pak porovnala s konvergentní majorantou 1/ k nadruhou.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#497 15. 09. 2019 17:23 — Editoval vanok (15. 09. 2019 19:13)
Re: Limitny maraton
A este mame podrobne
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#498 15. 09. 2019 17:25
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Kym som lateXoval, si prakticky popisala moje riesenie. 👍
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#499 15. 09. 2019 18:35 — Editoval jardofpr (15. 09. 2019 18:35)
Re: Limitny maraton
ahoj ↑ vanok:
vanok napsal(a):
LAhoj ↑ jardofpr:,
Pozor ... tvoja posledna rada diverguje. Tak nam to nic neda.
moznoze si len prehliadol mocninu, rada vpravo iste konverguje.
Inak tie riesenia mi pridu vlastne velmi podobne, aj co pise kolegyna.
Offline
#500 15. 09. 2019 18:45
Stránky: 1 … 18 19 20 21 22 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton

 ?
? .
. je konvergentna pre kazde
je konvergentna pre kazde  [tu treba povedat preco !]
[tu treba povedat preco !]

 .
. a
a





 a
a  vo funkcii
vo funkcii 

 v okoli
v okoli  a tak
a tak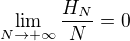 ]
]

 vyzera ze nie je problem ohranicit
vyzera ze nie je problem ohranicit  kladnou konstantou
kladnou konstantou kedze
kedze  aj
aj  rastu pomalsie ako
rastu pomalsie ako  potom
potom 
![kopírovat do textarea $S_n := \sum_{k=1}^n \int_k^{k+1} \frac{\mathrm{d}x}{x^{[x]}}\leq \sum_{k=1}^n\int_k^{k+1}\frac{\mathrm{d}x}{x^k}\leq\sum_{k=1}^n\int_k^{k+1}\frac{\mathrm{d}x}{k^k}=\sum_{k=1}^n\frac{1}{k^k}$](/mathtex/b5/b516457f3125cb7567365ad4db6fd4a5.gif)

![kopírovat do textarea $\frac 1{t ^{[x]}}$](/mathtex/5d/5d600e998f3e1506dd948638a66610d8.gif) je spojita po castiach a striktne kladna na
je spojita po castiach a striktne kladna na  ( tak je lokalne integtrabilna) a tiez
( tak je lokalne integtrabilna) a tiez ![kopírovat do textarea $\forall x \in [2, +\infty[, 0 < \frac 1{x^{[x]}} \leq \frac 1{x^2} $](/mathtex/e8/e8c2496bcdc61b4af6226166ea330c07.gif) .
.  konverguje, tak konverguje aj
konverguje, tak konverguje aj ![kopírovat do textarea $\int_{2}^{+\infty}\frac {dx}{x^{[x]}}$](/mathtex/74/746c39af239e93d6ccdbf3efebd07cb0.gif) .
.![kopírovat do textarea $\int_{1}^{+\infty}\frac {dx}{x^{[x]}}=\int_{1}^{2}\frac {dx}{x^{[x]}}+\int_{2}^{+\infty}\frac {dx}{x^{[x]}}$](/mathtex/fa/faaf7208f21e5725ac3bf90b51b182d4.gif) ukoncite [ lahko ukazeme, ze
ukoncite [ lahko ukazeme, ze ![kopírovat do textarea $\int_{1}^{2}\frac {dx}{x^{[x]}}$](/mathtex/1c/1c03262f97970204077398434ebccbca.gif) ...]
...] 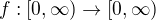 je rastúca konkávna funkcia.
je rastúca konkávna funkcia. a nech rad
a nech rad 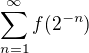 konverguje.
konverguje. konverguje.
konverguje.