Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 29. 05. 2009 20:09
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zjednodušení výrazu
Tenhle problém vzniknul zde
↑ musixx:
Proč by muselo platit  ?
?
↑ allergo: už neuvedl podmínky za kterých tuhle úpravu potřebujeme provést. Víme totiž, že  (pro nulové alfa musíme provést integraci zvlášť a dostaneme rovnou výsledek v požadovaném tvaru) a
(pro nulové alfa musíme provést integraci zvlášť a dostaneme rovnou výsledek v požadovaném tvaru) a  . Pak můžu upravovat
. Pak můžu upravovat
Offline
#5 01. 06. 2009 09:00 — Editoval musixx (01. 06. 2009 09:00)
Re: Zjednodušení výrazu
↑ BrozekP: Beru zpet - z nejakeho zahadneho duvodu jsem si nevsiml, ze v te zavorce pod odmocninou je jednou plus a jednou minus...
Offline

 ,
, 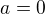 a
a 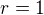 je
je  a
a  , tedy
, tedy  , zatimco
, zatimco  ).
).
