Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Odvozeni hustoty pravděpodobnosti pro normálni rozdělění
#1 18. 09. 2019 19:41
Odvozeni hustoty pravděpodobnosti pro normálni rozdělění
Má-li náhodná veličina  rozdělení
rozdělení 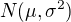 , distribuční funkci
, distribuční funkci  a hustotu pravděpodobnosti
a hustotu pravděpodobnosti  , pak:
, pak: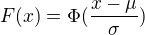 a
a 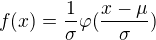 .
.
Odvodit distribucni funkci umim, ale zajímá mě odvození  :
:
Ve skriptech je nasledujici kratke odvozeni: 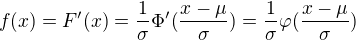 .
.
Nerozumim nasledujicimu kroku: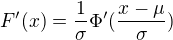
Proc je vytknuto  ? Derivovat a integrovat si myslim umim, ale tomuhle kroku nerozumim. Vite nekdo a umite to treba nejak rozepsat, aby to bylo videt?
? Derivovat a integrovat si myslim umim, ale tomuhle kroku nerozumim. Vite nekdo a umite to treba nejak rozepsat, aby to bylo videt?
Offline
#2 18. 09. 2019 19:47 — Editoval laszky (18. 09. 2019 19:49)
Re: Odvozeni hustoty pravděpodobnosti pro normálni rozdělění
↑ Andrew123:
Ahoj. Jedna se o derivaci slozene funkce 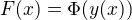 . Vnejsi funkce je
. Vnejsi funkce je 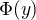 , vnitrni funkce je
, vnitrni funkce je 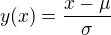 .
.
Plati: 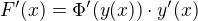 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Odvozeni hustoty pravděpodobnosti pro normálni rozdělění