Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 09. 2019 12:44 — Editoval jelena (20. 09. 2019 18:05)
- Matematik007

- Příspěvky: 31
- Reputace: 0
porozumenie prvému kroku
Edit: původní zadání a řešení je ze vzorových řešení korespondenčního semináře, ročník 2017/2018
https://sites.google.com/riesky.sk/prac … ie%C5%A1ky
z archivu:
Dobrý, vedel by mi niekto v následujúcej úlohe vysvetliť prečo rovnicu upravujeme do tvaru (R−k)(S −l) = m
Zadanie: Paľonardo vie, že v kráľovskom amfiteáteri musia byť všetky stoličky usporiadané do niekoľkých zarovnaných radov s rovnakým počtom stoličiek a teda musia tvoriť obdĺžnik. Musí na ne vedieť usadiť dámy a pánov nasledovne. V každom rade bude presne 14 pánov. V každom stĺpci bude presne 10 dám. Práve 3 stoličky budú prázdne. Ukážte, že stoličiek budú potrebovať najmenej 567. Riešenie: V prvom rade si uvedomme, čo znamená ukázať, že stoličiek budú potrebovať najmenej 567. Znamená to dokázať, že stoličiek nemôže byť menej ako 567 tak aby to vyhovovalo zadaniu. Neznamená to nájsť riešenie pre 567 stoličiek. Označme počet radov ako R a počet stĺpcov ako S. Kedže stoličky sú usporiadané v obdĺžniku, ich počet bude R·S. Počet pánov celkovo je 14R nakoľko ich je v každom rade 14, počet dám je podobným odvodením 10S a prázdne zostanú 3 stoličky. Preto pre počet stoličiek platí nasledujúca rovnica:
10S + 14R + 3 = RS (1)
Našim cieľom je zistiť pre aké dvojice R a S má zadanie riešenie. Následne budeme schopní vypočítať a nájsť najmenší súčin RS, teda počet stoličiek. Rovnicu 1 sa budeme snažiť upraviť do tvaru: (R−k)(S −l) = m (2) kde k, l a m sú čísla. Všimnime si, že ak roznásobíme zátvorky, dostaneme RS−lR−kS+kl. Z toho môžeme konštatovať l = 14, kedže v rovnici 1 je R násobené 14 a k = 10, nakoľko je S násobené 10. Násobok kl = 140 je o 3 menší ako m, takže m = 143. Pre lepšiu prehľadnosť si to vieme z rovnice 1 zapísať nasledovne: RS −14R−10S = 3 Z čoho odvodíme pripočítaním kl:
RS −14R−10S + kl = 3 + kl Ale naspäť k riešeniu. Rovnicu 2 sme upravili do tvaru: (R−10)(S −14) = 143 (3) Využijeme poznatok prvočíselného rozkladu čísla 143 = 11·13. Aby súčin zátvoriek v rovnici 3 bol rovný 143, musí nastať jeden z nasledujúcich štyroch prípadov: 1. (R−10) = 1 a (S −14) = 143 2. (R−10) = 11 a (S −14) = 13 3. (R−10) = 13 a (S −14) = 11 4. (R−10) = 143 a (S −14) = 1 V prvom prípade sa R = 11 a S = 157, v druhom R = 21 a S = 27, v treťom R = 23 a S = 25, a v poslednom štvrtom R = 153 a S = 15. Toto sú všetky možnosti počtu radov a stĺpcov v amfiteátri. V jednotlivých prípadoch bude počet stoličiek, teda RS: 1. 11·157 = 1727 2. 21·27 = 567 3. 23·25 = 575 4. 153·15 = 2295 Kedže v druhom prípade je počet stoličiek najmenší, bude to minimálny počet stoličiek. Ten je 567, čím sme dokázali, že v kráľovskom amfiteátri budú potrebovať najmenej 567 stoličiek.
Offline
#2 17. 09. 2019 12:49 — Editoval vlado_bb (17. 09. 2019 12:53)
Re: porozumenie prvému kroku
↑ Matematik007: Pretoze tento tvar nam umozni vyuzit rozklad cisla  (v tomto pripade
(v tomto pripade  ) na sucin prirodzenych cisel.
) na sucin prirodzenych cisel.
Offline
#3 17. 09. 2019 13:01 — Editoval Ferdish (17. 09. 2019 13:02)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: porozumenie prvému kroku
Inak vzhľadom na tú rovnicu (1) to vyzerá, že ide o pôvodné kompletné zadanie príkladu z tvojej predchádzajúcej témy a preto nerozumiem, prečo si nemohol pokračovať tam a musel si zakladať tému novú.
Offline
#4 19. 09. 2019 20:54
- Matematik007

- Příspěvky: 31
- Reputace: 0
Re: porozumenie prvému kroku
Ferdish
Ja tu hladám pomoc a nemusíte mi sem písať veci, ktoré mi vôbec nepomáhajú
PS. Tú novú tému som založil preto lebo som nechcel vyvolať zmätok, lebo som tam dal ako by ste tú rovnicu vyriešili a až potom som sem dal ako to bolo riešené a, že tomu nerozumiem
Offline
#5 19. 09. 2019 21:04
- Matematik007

- Příspěvky: 31
- Reputace: 0
Re: porozumenie prvému kroku
↑ vlado_bb:
Dik, ale odkiaľ tam dokázali, že l=14 a k=10
Lebo si nemyslím , že nato, že to tak je roznásobené v prvej rovnici to má byť roznásobené aj v rovnici 2
Offline
#6 19. 09. 2019 22:57 — Editoval jelena (20. 09. 2019 18:07)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: porozumenie prvému kroku
↑ Matematik007:
To vyplýva z vlastností polynómov (mnohočlenov). Rovnosti (1) a (2) sú vlastne reálne nenulové polynómy dvoch premenných, R a S.
Pre každé dva reálne nenulové polynómy platí, že ak sa majú rovnať, tak musia mať rovnaký stupeň (tj. hodnotu najvyššej mocniny nad premennou/premennými) a hodnoty koeficientov pri príslušných ekvivalentných členoch (teda členov s rovnakou mocninou jednej premennej alebo súčinom rovnakých mocnín oboch premenných) sa rovnajú.
Dúfam že si z toho niečo pochopil, nemám prehľad čo sa dnes ešte učí na ZŠ a čo nie, ale toto nevyzerá ako štandardná učebnicová úloha...odkiaľ ju máš, ak sa môžem spýtať?
Jelena: editováno
Offline


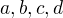 .
.