Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 19 20 21 22 23 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#501 15. 09. 2019 19:12 — Editoval vanok (16. 09. 2019 10:04)
Re: Limitny maraton
Ahoj ↑↑ jardofpr:, skutocne som to nepozorne cital.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#502 15. 09. 2019 21:16 — Editoval krakonoš (15. 09. 2019 23:48) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#503 15. 09. 2019 22:08 — Editoval misaH (16. 09. 2019 01:15)
#504 15. 09. 2019 22:34 — Editoval krakonoš (16. 09. 2019 00:07)
Re: Limitny maraton
↑ misaH:
Ahoj
Na tabletu je to v pohodě.
Asi mám moc velké prsty, připadá mi horor se trefit do těch mezer .A psát to rovnou v symbolech, to ještě zpaměti neumím.Příští týden to přepíšu- aspoň ty symboly co mám v textech.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#505 16. 09. 2019 01:13
#506 16. 09. 2019 08:46 — Editoval krakonoš (16. 09. 2019 15:48) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#507 16. 09. 2019 10:07
#508 16. 09. 2019 23:55 — Editoval krakonoš (17. 09. 2019 00:55)
Re: Limitny maraton
↑↑ jardofpr:
Ahoj.
Chtěla bych se zeptat na něco v zadání. už konverguje sama o sobě, podobně jako
už konverguje sama o sobě, podobně jako .
.
Aplikuji-li na členy konkávní funkci,není už automaticky řada konvergentní?V prvním kvadrantu lze vždy vzít linearní funkci y=kx, kde od určité chvíle bude konkávní funkce pod linearní funkcí??Aspoň u spojité f by to mělo platit, a pak už by i zadaná řada konvergovala.
Jedině si představuji, že je tam ta podmínka na konvergenci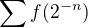 pro případy hodně nespojité f,definované pomocí jednostranných limit, a tato podmínka by zaručila, že takovou linearní funkci najdeme.Jinak nevím.
pro případy hodně nespojité f,definované pomocí jednostranných limit, a tato podmínka by zaručila, že takovou linearní funkci najdeme.Jinak nevím.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#509 17. 09. 2019 01:10 — Editoval jardofpr (17. 09. 2019 01:12)
Re: Limitny maraton
ahoj ↑ krakonoš:
spojitosť funkcie v zadaní nie je nijak vyhranená, t.j. spojitá byť môže a nemusí
aj preto ten predpoklad konvergencie radu s členmi 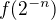
krakonoš napsal(a):
↑↑ jardofpr:
V prvním kvadrantu lze vždy vzít linearní funkci y=kx, kde od určité chvíle bude konkávní funkce pod linearní funkcí??Aspoň u spojité f by to mělo platit
tu si nie som úplne istý čo máš na mysli
Offline
#510 18. 09. 2019 08:23
Re: Limitny maraton
Ahojte, hint k (94):
Mozte napr. ukazat ze
inak zdá sa že predpoklad že
 má limitu nula idúc sprava k nule je zbytočný
má limitu nula idúc sprava k nule je zbytočný Offline
#511 19. 09. 2019 15:48 — Editoval krakonoš (19. 09. 2019 15:59)
Re: Limitny maraton
↑ jardofpr:
Ahoj.
Dovedu si představit funkce jako např ln(1+x), které mají tu vlastnost, že  .Pro tyto funkce bude tvrzení určitě platit.Takže pokud
.Pro tyto funkce bude tvrzení určitě platit.Takže pokud  , bude konvergence plynout z konvergentní majoranty.
, bude konvergence plynout z konvergentní majoranty.
Vzala jsem si ale funkci ![kopírovat do textarea $y=\sqrt[4]{a_{n}}$](/mathtex/ed/ed1112f16825847239ffdb7d84306d02.gif) , která je zaručeně rostoucí i konkávní, dále pak zvolila
, která je zaručeně rostoucí i konkávní, dále pak zvolila 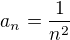 , tato řada konverguje a má nezáporné členy. Rovněž konverguje řada
, tato řada konverguje a má nezáporné členy. Rovněž konverguje řada ![kopírovat do textarea $\sum_{n=1}^{\infty }\sqrt[4]{2^{-n}}$](/mathtex/c9/c949d2819ce116341bf16019d85ff9c0.gif) , ale řada, kterou máme vyšetřit bude divergovat.Nebo někde dělám chybu?
, ale řada, kterou máme vyšetřit bude divergovat.Nebo někde dělám chybu?
Problém zřejmě není u hladkých funkcí, které jdou na okolí nuly rozvést v Taylorovu řadu, tam by se to mělo projevit střídavými znaménky a vlastností jakou jsem popsala u ln, aspoň se mi to tak na první pohled zdá.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#512 19. 09. 2019 16:03 — Editoval jardofpr (19. 09. 2019 16:03)
Re: Limitny maraton
ahoj ↑ krakonoš:
mne sa zdá že vyšetrovaný rad v príklade ktorý uvádzaš získa tvar 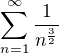
a tento bezpečne konverguje
Offline
#513 19. 09. 2019 16:07
Re: Limitny maraton
↑ jardofpr:
Díky, už to vidím, napsala jsem si integrál od 1 do nekonečna, a přitom pak dosadila meze od nuly do nekonećna,
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#514 19. 09. 2019 16:19 — Editoval krakonoš (19. 09. 2019 16:20)
Re: Limitny maraton
↑ jardofpr:
Mohu se ještě zeptat, jak jsi došel k té omezenosti shora?
U tohoto příkladu mě zarazilo, že je zde uvedena zrovna posloupnost  , protože kdybychom sečetli tuto řadu, bude součet toven jedné.Při konkávnosti by to vlastně mohlo být bráno jako váhy,dokázala by se ale konvergence řady
, protože kdybychom sečetli tuto řadu, bude součet toven jedné.Při konkávnosti by to vlastně mohlo být bráno jako váhy,dokázala by se ale konvergence řady  to ale nepomůže k vyřešení problému.
to ale nepomůže k vyřešení problému.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#515 19. 09. 2019 16:37 — Editoval jardofpr (19. 09. 2019 16:41)
Re: Limitny maraton
↑ krakonoš:
myslíš rozvinutie hintu v prispevku #510?
inak s tými váhami vôbec nie si ďaleko ak si tvoju úvahu správne interpretujem, dobrý postreh
nemal som inak v pláne to tu zamurovať, tak aby zostala dynamika,
jedno možné riešenie zajtra uvediem (ak ma nepredbehneš ;) )
Offline
#516 20. 09. 2019 13:53 — Editoval krakonoš (20. 09. 2019 14:05)
Re: Limitny maraton
↑ jardofpr:
Ahoj.
K tvému odhadu jsem se bohužel nedopracovala.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#517 20. 09. 2019 20:04 — Editoval jardofpr (20. 09. 2019 20:07)
Re: Limitny maraton
Ahojte
↑ krakonoš: možno že sa musím naučiť dávať lepšie hinty
aby to tu nestálo, možné riešenie problému (94)
Offline
#519 21. 09. 2019 11:32
Re: Limitny maraton
↑ jardofpr:
Ahoj.
Díky moc.Šlo mi hlavně o bližší vysvětlení té nerovnosti, kde osamostatňuješ f(a1)+f(a2) a používáš dvojnou sumu,už to vidím a chápu.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#520 21. 09. 2019 11:47
#521 22. 09. 2019 13:33
Re: Limitny maraton
↑ jardofpr:
Ahoj.
Já uvažovala log(n!)=log1+log2+...+logn,
a to je menší než n*(n+1)/2., menšence u rozdílu lze odhadnout tedy shora jedenáctou mocninou n, zatímco v menšiteli zůstává n!*log2, s rostoucím n je rozdíl víc a víc záporný a jde do mínus nekonečna.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#522 22. 09. 2019 16:39
#523 02. 10. 2019 07:11
#524 02. 10. 2019 11:28 — Editoval krakonoš (02. 10. 2019 11:55)
Re: Limitny maraton
↑ stuart clark:
Hi Stuart clark
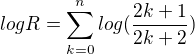
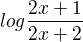 is increasing continuous negative function for
is increasing continuous negative function for 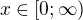

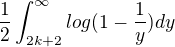 where k>0
where k>0

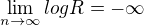
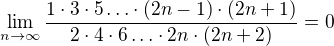
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#525 03. 10. 2019 16:21 — Editoval stuart clark (03. 10. 2019 16:25)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks ↑ krakonoš:
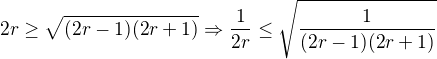
So 
Using Squeeze Theorem, 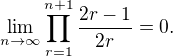
Offline
Stránky: 1 … 19 20 21 22 23 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
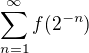
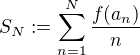 je neklesajúca a
je neklesajúca a 
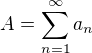 , iste platí
, iste platí 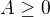 keďže
keďže  .
.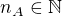 , že
, že  , a z toho
, a z toho 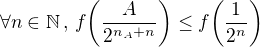 .
.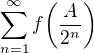 konverguje.
konverguje. 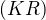
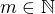 platí
platí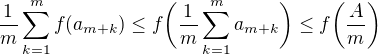

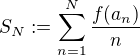
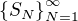 je zjavne neklesajúca keďže
je zjavne neklesajúca keďže 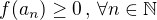 .
.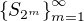 .
.![kopírovat do textarea $ S_{2^m} = \sum_{k=1}^{2^m}\frac{f(a_k)}{k}\leq f(a_1)+f(a_2) +\sum_{k=1}^{m-1}\frac{1}{2^k}\Bigg[\sum_{r=2^k+1}^{2^{k+1}}f(a_r)\Bigg] \stackrel{(JN)}{\leq} f(a_1)+f(a_2)+\sum_{k=1}^{m-1}f\bigg(\frac{A}{2^k}\bigg) \leq \dots$](/mathtex/6b/6bf72c341fd82af272054b722d41a434.gif)
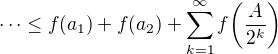
 teda má konečnú limitu a vyšetrovaný rad konverguje.
teda má konečnú limitu a vyšetrovaný rad konverguje.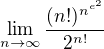
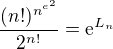 where
where 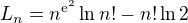
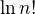 it should become clear that
it should become clear that 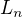 tends to minus infinity and limit we look for is equal to
tends to minus infinity and limit we look for is equal to 
