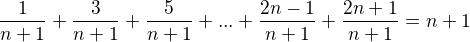Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 26. 09. 2019 22:45 — Editoval LordOfDav11 (26. 09. 2019 23:10)

LordOfDav11
Zelenáč
Příspěvky: 3
Škola: VŠB
Pozice: Student
Reputace:   0 
 

Příklad - Matematická indukce

Zdravím, vůbec si nevím rady jak pokračovat a nebo dělám někde chybu?

Zadání:
Dokažte matematickou indukcí:
$\forall n\in N, \frac{1}{n}+\frac{3}{n}+\frac{5}{n}+...+\frac{2n-1}{n}=n$

Pro n=1 platí L=P

Po použití indukce:
$n+\frac{2(n+1)-1}{n+1}=n+1$
$n+\frac{2n+1}{n+1}=n+1$

Děkuji za případnou pomoc.

Offline

  • (téma jako vyřešené označil(a) LordOfDav11)

#2 26. 09. 2019 23:03 — Editoval kerajs (26. 09. 2019 23:05)

kerajs
Příspěvky: 235
Reputace:   20 
 

Re: Příklad - Matematická indukce

LordOfDav11 napsal(a):

Po použití indukce:
$n+\frac{2(n+1)-1}{n}=n+1$
$n+\frac{2n+1}{n}=n+1$

1)
$\frac{1}{n+1}+\frac{3}{n+1}+\frac{5}{n+1}+...+\frac{2n-1}{n+1}+\frac{2n+1}{n+1}=n+1 $
2)
$\frac{1}{n+1}+\frac{3}{n+1}+\frac{5}{n+1}+...+\frac{2n-1}{n+1}=\frac{n^2}{n+1}\neq n$

Offline

 

#3 26. 09. 2019 23:13 — Editoval vanok (26. 09. 2019 23:16)

vanok
Příspěvky: 14450
Reputace:   741 
 

Re: Příklad - Matematická indukce

Ahoj ↑ LordOfDav11:, to trochu oprav

n=1, to mas dobre. 

Ale indukcny krok je toto :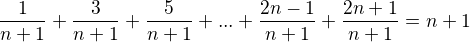

$ \frac{1}{n+1}+\frac{3}{n+1}+\frac{5}{n+1}+...+\frac{2n-1}{n+1}+ \frac {2n+1}{n+1} =n+1$
( v celom vyroku, musis nahradit n cislom n+1)

Skus to dokazat tak ze pouzijes tvoj prvy vzorec.

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#4 27. 09. 2019 01:02

Pomeranc
Příspěvky: 682
Pozice: student
Reputace:   10 
 

Re: Příklad - Matematická indukce

LordOfDav11 napsal(a):

Zdravím, vůbec si nevím rady jak pokračovat a nebo dělám někde chybu?

Zadání:
Dokažte matematickou indukcí:
$\forall n\in N, \frac{1}{n}+\frac{3}{n}+\frac{5}{n}+...+\frac{2n-1}{n}=n$

Pro n=1 platí L=P

Po použití indukce:
$n+\frac{2(n+1)-1}{n+1}=n+1$
$n+\frac{2n+1}{n+1}=n+1$

Děkuji za případnou pomoc.

Já se taky přidám :).

Pro n=1 to zvládneš. Pak si řekněme.

Víme, že to platí pro n a chceme dokázat, že to platí to n+1.
Pro n to vypadá:
$\forall n\in N, \frac{1}{n}+\frac{3}{n}+\frac{5}{n}+...+\frac{2n-1}{n}=n$
Je to náš indukční předpoklad.

Pro n+1 to vypadá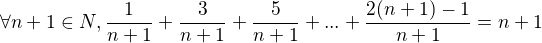
$\forall n+1\in N, \frac{1}{n+1}+\frac{3}{n+1}+\frac{5}{n+1}+...+\frac{2(n+1)-1}{n+1}=n+1$

Pak se vezme pravá nebo levá část z rovnice n+1 a upravuje se to a využije se indukčního předpokladu, až pak dostanu druhou část rce.

Pro inspiraci se můžeš podívat zde: Odkaz

Offline

 

#5 29. 09. 2019 09:00

LordOfDav11
Zelenáč
Příspěvky: 3
Škola: VŠB
Pozice: Student
Reputace:   0 
 

Re: Příklad - Matematická indukce

Tak bohužel, vůbec si s tím nevím rady. To mám jako 1/(n+1) rozdělit, tak aby mi vyšlo 1/n + něco?

Offline

 

#6 29. 09. 2019 09:36 — Editoval vanok (29. 09. 2019 09:53)

vanok
Příspěvky: 14450
Reputace:   741 
 

Re: Příklad - Matematická indukce

Ahoj,
Skor ako eacnes riesit toto cvicenie, mozes ho napisat trochu praktickejsie. (Co nic nezmeni na veci!)
Miesto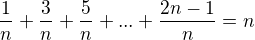
$ \frac{1}{n}+\frac{3}{n}+\frac{5}{n}+...+\frac{2n-1}{n}=n$
mozes napisat
$ \frac{{1}+{3}{n}+{5}{n}+...+{2n-1}}{n}=\frac {n^2}n=n$  $(P_n)$.
Dokaz indukciou spociva:
Dokazes 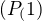$(P_(1)$.( co si uz urobil.)
Indukcny krok spociva v dokaze: ze $(P_n)$ implikuje $(P_{n+1})$.
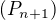[ ked dokazes tie dve etapy, mozes povedat, ze $(P_n)$ plati pre vsetky 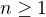$n \ge1$]
Skus to urobit.   ( alebo aspon napis tvoj pokus).

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#7 29. 09. 2019 09:54

kerajs
Příspěvky: 235
Reputace:   20 
 

Re: Příklad - Matematická indukce

$L= \frac{1}{n+1}+\frac{3}{n+1}+\frac{5}{n+1}+...+\frac{2n-1}{n+1}+\frac{2n+1}{n+1}=\frac{1+3+...+(2n-1)+(2n+1)}{n+1}=\\= \frac{n(\frac{1+3+...+(2n-1)}{n})+(2n+1)}{n+1}= \frac{n\cdot n+(2n+1)}{n+1}= \frac{(n+1)^2}{n+1}=n+1=P$

Offline

 

#8 29. 09. 2019 10:18

vanok
Příspěvky: 14450
Reputace:   741 
 

Re: Příklad - Matematická indukce

Ahoj ↑ kerajs:,
Iste sa ti podakuje kolega ↑ LordOfDav11:.  ( som dufal, ze to mohol aj on sam nast).

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#9 29. 09. 2019 10:46

kerajs
Příspěvky: 235
Reputace:   20 
 

Re: Příklad - Matematická indukce

Bohužel, toto fórum nemá fičúrku, ktorá pri odosielaní odpovede upozorní na nové príspevky, ktoré medzitým odoslal niekto iný. Sorry.

Offline

 

#10 29. 09. 2019 11:33

vlado_bb
Moderátor
Příspěvky: 6211
Škola:
Reputace:   142 
 

Re: Příklad - Matematická indukce

↑ kerajs: V takom pripade by som vyuzil moznost zmazania vlastneho prispevku, zvlast v tomto pripade, ked ↑ vanok: poskytol RADU, kym ty v ↑ kerajs: UPLNE RIESENIE (co je mimochodom v rozpore s platnymi pravidlami a odporucaniami).

Offline

 

#11 29. 09. 2019 11:35

vanok
Příspěvky: 14450
Reputace:   741 
 

Re: Příklad - Matematická indukce

Ahoj ↑ kerajs:,
Vsak si dobre urobil. 
A nase prispevky sa doplnuju. 

Peknu nedelu.

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#12 29. 09. 2019 14:10

LordOfDav11
Zelenáč
Příspěvky: 3
Škola: VŠB
Pozice: Student
Reputace:   0 
 

Re: Příklad - Matematická indukce

Tak děkuji všem za vaše rychlé a užitečné nápovědy (i řešení :D).

Offline

 

#13 07. 10. 2019 22:44

jelena
Jelena
Místo: Opava
Příspěvky: 30020
Škola: MITHT (abs. 1986)
Pozice: plním požadavky ostatních
Reputace:   100 
 

Re: Příklad - Matematická indukce

↑ kerajs:

Zdravím,

Bohužel, toto fórum nemá fičúrku, ktorá pri odosielaní odpovede upozorní na nové príspevky, ktoré medzitým odoslal niekto iný. Sorry.

pomůže použití tlačítka Náhled (kterým se kontroluje příspěvek před odesláním), potom pod oknem s vlastním příspěvkem je vidět všechny dosud přidané příspěvky vč. toho, který byl přidán během psání. Víz téma, děkuji.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson