Matematické Fórum

xstudentíkx · 12. 10. 2019 13:26

Ahojky,

nenapadá někoho jak by se dala jednoduše vyřešit tato úloha:
2 hráči hází 3 kostkami. Při stejné hodnotě se hra anuluje, kdo hodí víc, vyhrál.
Já házím první a hodím součet 13, jaká je pravděpodobnost, že vyhraji?

Jedním řešením je vypsat si všechny možnosti, kdy vyhraji, tedy když mu padne 12 a méně a podělit to 6^3. Nicméně neexistuje na to nějaký fígl?

Děkuji.

Ferdish · 12. 10. 2019 14:57

Skôr jednoduchšie je spočítať pp prehry (tj keď protihráč hodí 14 a viac) a to potom odčítať od jedničky.

A tiež pozor, všetkých hodov nie je 6^3 - to by platilo v prípade, keby záležalo na poradí, ktoré číslo padne na ktorej kocke (ak by bolo možné ich navzájom rozlíšiť). Túto podmienku však zadanie príkladu vôbec nepožaduje. Napr. ak by mi na dvoch kockách padlo 6 a na jednej 3 a nejako si ich zoradím vedľa seba, tak mi je jedno či ich mám zoradené 3-6-6, 6-3-6 alebo 6-6-3. Je to jeden a ten istý výsledný hod.

Stýv · 12. 10. 2019 15:13

↑ Ferdish: Jenže např. 366 a 666 mají různou pst, takže je třeba počítat to, jako by na pořadí záleželo.

xstudentíkx · 12. 10. 2019 15:20

↑ Ferdish:

Jo to je určitě jednodušší, ale i tak musím vypsat spoustu možností, myslela jsem, jestli není nějaký postup, že třeba PP součtu 10 je největší a pak nějak využít symetrie, ale to asi nepůjde.

↑ Stýv:

Také si myslím, takže to budu normálně dělit 6*6*6, neboli všemi možnostmi, které mohou nastat, že ano?

Ferdish

↑ Stýv:
Načo uvažovať pp-i jednotlivých hodov? Nehľadáme pravdepodobnosť želaného javu ako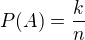

$P(A)=\frac{k}{n}$

prípadne ako

$P(A)=1-\frac{l+m}{n}$

kde $k$ je počet možných hodov pre nás priaznivých (protihráčovi padne 12 a menej), $l$ je počet možných hodov kedy nastane remíza resp. anulácia (protihráčovi padne presne 13) ktorá sa však nepovažuje za výhru (to mi v mojej pôvodnej úvahe uniklo, za čo sa ospravedlňujem), $m$ je počet možných hodov pre nás nepriaznivých (protihráčovi padne 14 a viac) a $n$ je počet všetkých možných hodov?

Hodnoty všetkých štyroch koeficientov by šli vyjadriť buď pomocou kombinačných čísiel alebo vzorcov s ich použitím..aspoň mne sa zdá, že sa tam nádherne uplatnia kombinácie s opakovaním.

Ale priznávam, že úlohy z kombinatoriky resp. úlohy kde sa používajú úvahy s využitím kombinačných čísiel a vzorcov boli vždy moja slabina, takže mi možno niečo uniká...

Jj · 13. 10. 2019 09:02 — Editoval Jj (13. 10. 2019 09:04)

↑ xstudentíkx:

Hezký den.

Pokud jde o určení četnosti možných ciferných součtů, tak s tím si já nedovedu poradit bez počítače:

Hledáme počty trojic celých čísel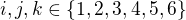

$i, j, k \in \{1, 2, 3, 4, 5, 6\}$ , které splňují vztahy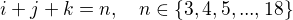

$i+j+k = n, \quad n\in \{3, 4, 5, ..., 18\}$

1. Projít postupně všechna trojciferná čísla s uvedenými ciframi a četnosti jednoduše nasčítat. Nalezené četnosti jsou (ve vzestupném pořadí) tyto:

1,3,6,10,15,21,25,27,27,25,21,15,10,6,3,1

2. Četnosti se rovnají koeficientům u jednotlivých mocnin proměnné x v umocněnému výrazu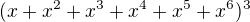

$(x+x^2+x^3+x^4+x^5+x^6)^3$ , seřazeném podle mocnin x:

Viz WA: Odkaz

Pořadí koeficientů obecně od nejnižší mocniny, ale v tomto případě jsou koeficienty rozložený symetricky, takže je to jedno. Výsledek je stejný jako v odstavci 1.

Stýv · 13. 10. 2019 09:41

↑ Ferdish: Tak si to zkus spočítat na jednoduším případě - mně padlo v součtu 5, jaká je pst, že vyhraju (tj. že soupeři padne 3 nebo 4)?

Matematické Fórum

#1 12. 10. 2019 13:26

Pravděpodobnost - kostky

#2 12. 10. 2019 14:57

Re: Pravděpodobnost - kostky

#3 12. 10. 2019 15:13

Re: Pravděpodobnost - kostky

#4 12. 10. 2019 15:20

Re: Pravděpodobnost - kostky

#5 13. 10. 2019 02:59 — Editoval Ferdish (13. 10. 2019 03:09)

Re: Pravděpodobnost - kostky

#6 13. 10. 2019 09:02 — Editoval Jj (13. 10. 2019 09:04)

Re: Pravděpodobnost - kostky

#7 13. 10. 2019 09:41

Re: Pravděpodobnost - kostky

Zápatí