Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 10. 2016 15:00 — Editoval Rumburak (18. 10. 2016 15:57)
Re: Důkaz
↑ aniuce:
Ahoj. Zkusil bych zkoumat úhly.
Mějme tedy ostroúhlý trojúhelník 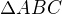 s tradičním označením stran a úhlů. Označme dále
s tradičním označením stran a úhlů. Označme dále 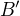 patu výšky z bodu
patu výšky z bodu 
a 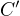 patu výšky z bodu
patu výšky z bodu  . Dostaneme trojúhelník
. Dostaneme trojúhelník  (mající ovšem "cyklickou orientací" opačnou než
(mající ovšem "cyklickou orientací" opačnou než 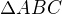 )
)
s úhly  po řadě odpovídajícími příslušným vrcholům. Snažme se dokázat, že
po řadě odpovídajícími příslušným vrcholům. Snažme se dokázat, že
(1)  .
.
Je zřejmé, že  , takže ze vztahů (1) už stačí dokázat pouze jeden.
, takže ze vztahů (1) už stačí dokázat pouze jeden.
Offline
#3 18. 10. 2016 17:56
Re: Důkaz
Ahoj ↑ aniuce:,
Tu je dobre pouzit orticky trojuholnik
Oznac päty vysok  ( tie tvoria orticky trojuholnik)
( tie tvoria orticky trojuholnik)
Nakresli si to a vyuzi kocyklicke stvorice bodov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 18. 10. 2016 22:42 — Editoval Eratosthenes (18. 10. 2016 22:43)
#5 18. 10. 2016 23:03 — Editoval vanok (19. 10. 2016 00:59)
Re: Důkaz
Tu ↑ vanok: som pisal o kocyklickych bodoch. To sa da pouzit napr. takto  su kocyklicke.
su kocyklicke.
Tak  .
.
Poznamka . Co kolega znaci napr. 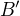 ja znacim
ja znacim  ... atd.
... atd.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 30. 10. 2019 14:31
Re: Důkaz
↑ Rumburak:
Dobrý den,
mohla bych Vás poprosit, zda byste mi neporadil s dalším postupem při řešení příkladu? Začátek jsem pochopila, ale nevím si moc rady, jak dál..
Děkuji!
Offline
#7 31. 10. 2019 00:23
Re: Důkaz
↑ Johana16:
Např. takto. Označme S střed strany BC a uvažme trojúhelník SB'C', ten je rovnoramenný (proč?). Stejně tak jsou rovnoramenné trojúhelníky SBC' a SB'C. Odtud plyne 
a stejně tak
odkud jednoduchý dopočtem do přímého úhlu (nebo nahlédnutím :)) .
.
Protože je trojúhelník B'SC' rovnoramenný, dostáváme, že .
.
Ale odtud už plyne  .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline


 = ABC ~ AC'B' (sus)
= ABC ~ AC'B' (sus)